题目内容
设圆C的方程x2+y2-2x-2y-2=0，直线l的方程（m+1）x-my-1=0，对任意实数m，圆C与直线l的位置关系是________．
相交
分析：求出直线恒过的定点，确定点与圆心的距离与半径的关系，推出结论．
解答：由直线l的方程（m+1）x-my-1=0，可得m（x-y）+x-1=0，直线恒过（1，1）点，
圆C的方程x2+y2-2x-2y-2=0，的圆心（1，1），
所以圆C与直线l的位置关系是：相交
故答案为：相交
点评：本题考查直线与圆的位置关系，考查计算能力，是基础题．
分析：求出直线恒过的定点，确定点与圆心的距离与半径的关系，推出结论．
解答：由直线l的方程（m+1）x-my-1=0，可得m（x-y）+x-1=0，直线恒过（1，1）点，
圆C的方程x2+y2-2x-2y-2=0，的圆心（1，1），
所以圆C与直线l的位置关系是：相交
故答案为：相交
点评：本题考查直线与圆的位置关系，考查计算能力，是基础题．
练习册系列答案
相关题目
，
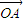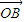满足
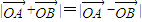，设圆C的方程为x2+y2-（x1+x2）x-（y1+y2）y=0．
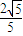时，求p的值．
，
满足
，设圆C的方程为x2+y2-（x1+x2）x-（y1+y2）y=0．
时，求p的值．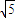
时，求P的值．