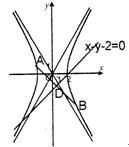
题目内容
已知双曲线
的离心率e=2，A，B为双曲线上两点，线段AB的垂直平分线为
①求双曲线C经过二、四象限的渐近线的倾斜角
②试判断在椭圆C的长轴上是否存在一定点N（a，0），
使椭圆上的动点M满足
的最小值为3，若存在求出所有可能的a值，若不存在说明理由.
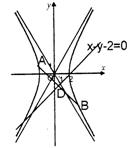
①解由e=2，得
…………1分
所以双曲线C经过二、四象限的渐近线的倾斜角为
……2分
②设
，B（
），D
代入双曲线方程相减得
…………4分
∴
…………6分
将AB的方程 
………………8分
由|AB|=
，计算得 
所以双曲线C的方程为 
…………12分
解析:
同答案
练习册系列答案
相关题目
的离心率e＝2，且
、
分别是双曲线虚轴的上、下端点
（
，
），求双曲线的方程；
、
是双曲线上不同的两点，且
，求直线
的方程
的离心率e=2，A，B为双曲线上两点，线段AB的垂直平分线为
的最小值为3，若存