题目内容
已知m、l是两条不同直线,α、β是两个不同平面,给出下列说法:
①若l垂直于α内两条相交直线,则l⊥α;
②m?α,l?β,且l⊥m,则α⊥β;
③若l?β,且l⊥α,则α⊥β;
④若m?α,l?β,且α∥β,则l∥m.
其中正确的序号是
①若l垂直于α内两条相交直线,则l⊥α;
②m?α,l?β,且l⊥m,则α⊥β;
③若l?β,且l⊥α,则α⊥β;
④若m?α,l?β,且α∥β,则l∥m.
其中正确的序号是
①③
①③
.分析:对于①,由直线与平面垂直的判定定理能够判断真假;
对于②,由平面与平面垂直的判定定理知α与β不一定垂直;
对于③,由平面与平面垂直的判定定理知α与β一定垂直;
对于④,由平面与平面平行的性质知m∥l或m与l异面.
对于②,由平面与平面垂直的判定定理知α与β不一定垂直;
对于③,由平面与平面垂直的判定定理知α与β一定垂直;
对于④,由平面与平面平行的性质知m∥l或m与l异面.
解答:解:①l垂直于α内的两条相交直线,由直线与平面垂直的判定定理知l⊥α,故①正确;
②若m?α,l?β且l⊥m,则α与β不一定垂直.故②不正确;
③若l?β,l⊥α,则由平面与平面垂直的判定定理知α⊥β,故③正确;
④若m?α,l?β且α∥β,则m∥l或m与l异面,故④不正确.
故答案为:①③
②若m?α,l?β且l⊥m,则α与β不一定垂直.故②不正确;
③若l?β,l⊥α,则由平面与平面垂直的判定定理知α⊥β,故③正确;
④若m?α,l?β且α∥β,则m∥l或m与l异面,故④不正确.
故答案为:①③
点评:本题考查直线与直线、直线与平面、平面与平面间的位置关系的判断,是基础题.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
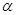 、
、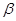 是两个不同平面,给出下列说法:
是两个不同平面,给出下列说法: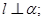
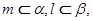 且
且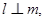 则
则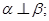
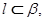 且
且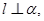 则
则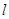 ∥
∥