题目内容
过椭圆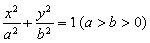 的左顶点
的左顶点 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与 轴的交点为
轴的交点为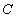 ,已知
,已知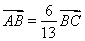 .
.
(1)求椭圆的离心率;
(2)设动直线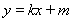 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点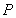 ,且与直线
,且与直线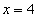 相交于点
相交于点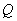 ,若
,若 轴上存在一定点
轴上存在一定点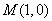 ,使得
,使得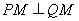 ,求椭圆的方程.
,求椭圆的方程.
【答案】
(1)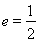 ;(2)
;(2)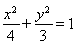 .
.
【解析】
试题分析:(I)根据
 ,设直线方程为
,设直线方程为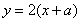 ,
,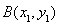
确定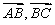 的坐标,由
的坐标,由 确定得到
确定得到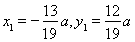 ,
,
再根据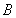 点在椭圆上,求得
点在椭圆上,求得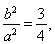 进一步即得所求
进一步即得所求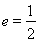 ;
;
(2)由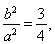 可设
可设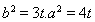 ,
,
得到椭圆的方程为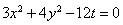 ,
,
由 得
得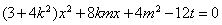
根据动直线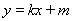 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
得到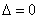 ,整理得
,整理得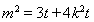 .
.
确定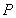 的坐标
的坐标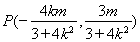 ,
,
又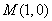 ,
, 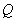
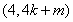
若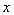 轴上存在一定点
轴上存在一定点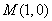 ,使得
,使得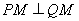 ,那么
,那么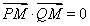
可得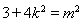 ,由
,由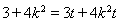 恒成立,故
恒成立,故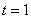 ,得解.
,得解.
试题解析:(1)∵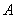
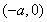 ,设直线方程为
,设直线方程为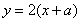 ,
,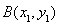
令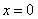 ,则
,则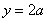 ,∴
,∴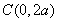 , 2分
, 2分
∴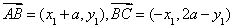 3分
3分
∵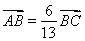 ,∴
,∴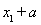 =
=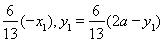 ,
,
整理得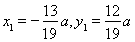 4分
4分
∵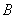 点在椭圆上,∴
点在椭圆上,∴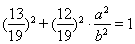 ,∴
,∴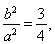 5分
5分
∴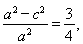 即
即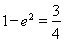 ,∴
,∴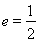 6分
6分
(2)∵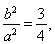 可设
可设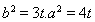 ,
,
∴椭圆的方程为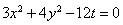 7分
7分
由 得
得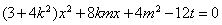 8分
8分
∵动直线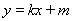 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
∴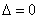 ,即
,即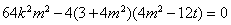
整理得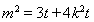 9分
9分
设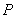
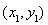 则有
则有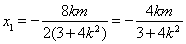 ,
,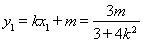
∴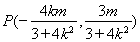 10分
10分
又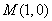 ,
,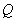
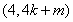
若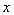 轴上存在一定点
轴上存在一定点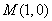 ,使得
,使得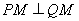 ,
,
∴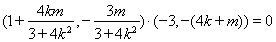 恒成立
恒成立
整理得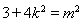 , 12分
, 12分
∴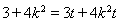 恒成立,故
恒成立,故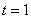
所求椭圆方程为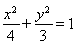 13分
13分
考点:椭圆的几何性质,直线与圆锥曲线的位置关系,共线向量,平面向量垂直的充要条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为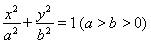
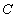
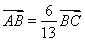
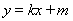
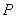
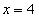
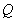
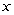

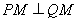
 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.