题目内容
已知函数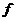 (
(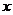 ) =
) =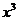 ,g (
,g (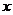 )=
)=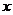 +
+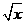 。
。
(Ⅰ)求函数h (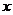 )=
)=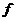 (
(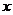 )-g (
)-g (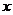 )的零点个数,并说明理由;
)的零点个数,并说明理由;
(Ⅱ)设数列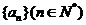 满足
满足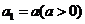 ,
,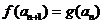 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的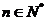 ,都有
,都有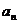 ≤
≤ 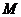 .
.
【答案】
解析:(I)由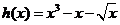 知,
知, ,而
,而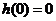 ,且
,且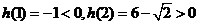 ,则
,则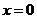 为
为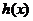 的一个零点,且
的一个零点,且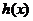 在
在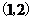 内有零点,因此
内有零点,因此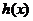 至少有两个零点
至少有两个零点
解法1: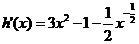 ,记
,记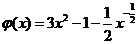 ,则
,则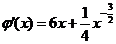 。
。
当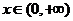 时,
时,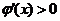 ,因此
,因此 在
在 上单调递增,则
上单调递增,则 在
在 内至多只有一个零点。又因为
内至多只有一个零点。又因为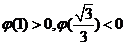 ,则
,则 在
在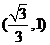 内有零点,所以
内有零点,所以 在
在 内有且只有一个零点。记此零点为
内有且只有一个零点。记此零点为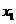 ,则当
,则当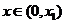 时,
时,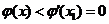 ;当
;当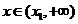 时,
时,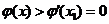 ;
;
所以,
当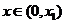 时,
时,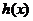 单调递减,而
单调递减,而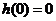 ,则
,则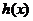 在
在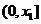 内无零点;
内无零点;
当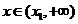 时,
时,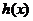 单调递增,则
单调递增,则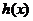 在
在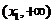 内至多只有一个零点;
内至多只有一个零点;
从而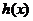 在
在 内至多只有一个零点。综上所述,
内至多只有一个零点。综上所述,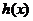 有且只有两个零点。
有且只有两个零点。
解法2: ,记
,记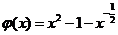 ,则
,则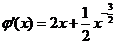 。
。
当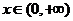 时,
时,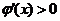 ,因此
,因此 在
在 上单调递增,则
上单调递增,则 在
在 内至多只有一个零点。因此
内至多只有一个零点。因此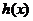 在
在 内也至多只有一个零点,
内也至多只有一个零点,
综上所述,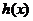 有且只有两个零点。
有且只有两个零点。
(II)记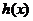 的正零点为
的正零点为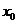 ,即
,即 。
。
(1)当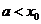 时,由
时,由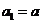 ,即
,即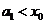 .而
.而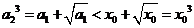 ,因此
,因此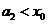 ,由此猜测:
,由此猜测: 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当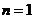 时,
时,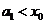 显然成立;
显然成立;
②假设当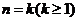 时,有
时,有 成立,则当
成立,则当 时,由
时,由
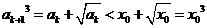 知,
知,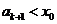 ,因此,当
,因此,当 时,
时,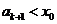 成立。
成立。
故对任意的 ,
, 成立。
成立。
(2)当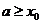 时,由(1)知,
时,由(1)知,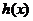 在
在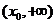 上单调递增。则
上单调递增。则 ,即
,即 。从而
。从而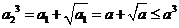 ,即
,即 ,由此猜测:
,由此猜测: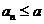 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当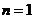 时,
时, 显然成立;
显然成立;
②假设当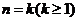 时,有
时,有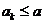 成立,则当
成立,则当 时,由
时,由
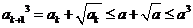 知,
知,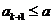 ,因此,当
,因此,当 时,
时,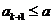 成立。
成立。
故对任意的 ,
,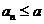 成立。
成立。
综上所述,存在常数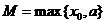 ,使得对于任意的
,使得对于任意的 ,都有
,都有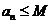 .
.

练习册系列答案
相关题目
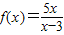 ,f[g(x)]=4-x.
,f[g(x)]=4-x.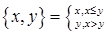 。已知函数
。已知函数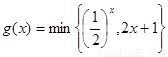 ,则g(x)的最大值为______。
,则g(x)的最大值为______。