题目内容
不论a为何值时,函数y=(a-1)2x-
恒过一定点,这个定点坐标是( )
| a |
| 2 |
A、(1,-
| ||
B、(1,
| ||
C、(-1,-
| ||
D、(-1,
|
分析:由已知中,不论a为何值时,函数y=(a-1)2x-
恒过一定点,我们可将函数的解析式变形为(2x-
)a-(2x+y)=0的形式,则根据2x-
=0,2x-y=0,构造一个关于x,y的方程,解方程即可求出定点坐标.
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:函数y=(a-1)2x-
的解析式可化为
(2x-
)a-(2x+y)=0
若不论a为何值时,函数y=(a-1)2x-
恒过一定点,
即不论a为何值时,(2x-
)a-(2x+y)=0恒成立
则2x-
=0,2x+y=0
解得x=-1,y=-
,即恒过的定点坐标是(-1,-
)
故选C.
| a |
| 2 |
(2x-
| 1 |
| 2 |
若不论a为何值时,函数y=(a-1)2x-
| a |
| 2 |
即不论a为何值时,(2x-
| 1 |
| 2 |
则2x-
| 1 |
| 2 |
解得x=-1,y=-
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查的知识点是函数图象过点,处理的方法是将函数的解析式化成两部分:一部分含参数,一部分不含参数,让两部分的系数均为0,构造方程组.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
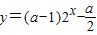 恒过一定点,这个定点坐标是( )
恒过一定点,这个定点坐标是( )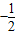 )
) )
) )
) )
)