题目内容
定义在R上的函数 ,
, 满足
满足 ,
,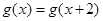 ,若
,若 且
且 ,则
,则 =____.
=____.
2
解析试题分析:由 ,
, ,可知
,可知 为奇函数,令
为奇函数,令 可得
可得 ;若
;若 则
则 ,又
,又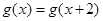 ,所以
,所以 代入到
代入到 ,可得
,可得 ,取
,取 ,则
,则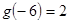 ,所以
,所以 =2.
=2.
考点:函数的奇偶性、周期性.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
题目内容
定义在R上的函数 ,
, 满足
满足 ,
,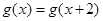 ,若
,若 且
且 ,则
,则 =____.
=____.
2
解析试题分析:由 ,
, ,可知
,可知 为奇函数,令
为奇函数,令 可得
可得 ;若
;若 则
则 ,又
,又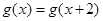 ,所以
,所以 代入到
代入到 ,可得
,可得 ,取
,取 ,则
,则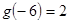 ,所以
,所以 =2.
=2.
考点:函数的奇偶性、周期性.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案