题目内容
6.已知数列{an},满足a1=4,an+1=3an-4,(n∈N*),求该数列的通项公式.分析 根据题意,由an+1=3an-4,可得an+1-2=3(an-2),结合a1-2=2可得数列{an-2}是以a1-2=2为首项,公比q=3的等比数列;由等比数列的通项公式可得an-2=2×3n-1,变形可得an=2×3n-1+2,即可得答案.
解答 解:根据题意,由an+1=3an-4,可得an+1-2=3an-6=3(an-2),
即an+1-2=3(an-2),a1-2=2,
则数列{an-2}是以a1-2=2为首项,公比q=3的等比数列,
则an-2=2×3n-1;
则an=2×3n-1+2;
故数列的通项公式为an=2×3n-1+2.
点评 本题考查数列的递推公式的运用,关键是分析an+1=3an-4,变形得到an+1与an的关系.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
15.若2cos($\frac{π}{2}$-α)-sin($\frac{3}{2}$π+α)=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
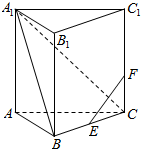 如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.
如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C. 已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )