题目内容
一企业的某产品每件利润100元,在未做电视广告时,日销售量为b件.当对产品做电视广告后,记每日播n次时的日销售量为an(n∈N*)件,调查发现:每日播一次则日销售量al件b件的基础上增加
件,每日播二次则日销售量a2件在每日播一次时日销售量al件的基础上增加
件…,每日播n次,该产品的该产品的日销售an件在每日播n-1次时的日销售量件an-1的基础上增加
件.合同约定:每播一次企业需支付广告费2b元.
(Ⅰ)试求出an与n的关系式;
(Ⅱ)该企业为了获得扣除广告费后的日利润最大,求每日电视广告需播多少次.
| b |
| 2 |
| b |
| 4 |
| b |
| 2n |
(Ⅰ)试求出an与n的关系式;
(Ⅱ)该企业为了获得扣除广告费后的日利润最大,求每日电视广告需播多少次.
分析:(Ⅰ)根据每日播一次则日销售量al件b件的基础上增加
件,每日播二次则日销售量a2件在每日播一次时日销售量al件的基础上增加
件…,每日播n次,该产品的该产品的日销售an件在每日播n-1次时的日销售量件an-1的基础上增加
件,可得递推关系,再采用等比数列的求和公式,即可求出an与n的关系式;
(Ⅱ)求出企业为了获得扣除广告费后的日利润,确定其单调性,即可得出结论.
| b |
| 2 |
| b |
| 4 |
| b |
| 2n |
(Ⅱ)求出企业为了获得扣除广告费后的日利润,确定其单调性,即可得出结论.
解答:解:(Ⅰ)设电视广告播放量为每天i次时,该产品的销售量为为ai(0≤i≤n,).
由题意,ai=
,
∴an=b+(
+
+…+
)=b(2-
),
所以,该产品每天销售量an(件)与电视广告播放量n(次/天)的函数关系式为an=b(2-
),n∈N*.
(Ⅱ)设该企业为了获得扣除广告费后的日利润最大,每日电视广告需播n次.
则有cn=100b(2-
)-2bn=100b(2-0.02n-
)
∵cn-cn-1= 100b(0.02-
)≥0,∴2n≤50,∴n≤5
∵cn+1-cn= 100b(0.02-
)≤0,∴2n≥25,∴n≥5
∴n=5
∴要使设该企业为了获得扣除广告费后的日利润最大,每日电视广告需播5次
由题意,ai=
|
∴an=b+(
| b |
| 2 |
| b |
| 22 |
| b |
| 2n |
| 1 |
| 2n |
所以,该产品每天销售量an(件)与电视广告播放量n(次/天)的函数关系式为an=b(2-
| 1 |
| 2n |
(Ⅱ)设该企业为了获得扣除广告费后的日利润最大,每日电视广告需播n次.
则有cn=100b(2-
| 1 |
| 2n |
| 1 |
| 2n |
∵cn-cn-1= 100b(0.02-
| 1 |
| 2n |
∵cn+1-cn= 100b(0.02-
| 1 |
| 2n+1 |
∴n=5
∴要使设该企业为了获得扣除广告费后的日利润最大,每日电视广告需播5次
点评:本题考查函数模型的建立与运用,考查函数的单调性,考查学生阅读分析问题的能力,综合性强.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
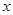 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为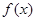 万元,且
万元,且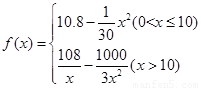
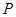 (万元)关于年产品
(万元)关于年产品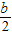 件,每日播二次则日销售量a2件在每日播一次时日销售量al件的基础上增加
件,每日播二次则日销售量a2件在每日播一次时日销售量al件的基础上增加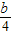 件…,每日播n次,该产品的该产品的日销售an件在每日播n-1次时的日销售量件an-1的基础上增加
件…,每日播n次,该产品的该产品的日销售an件在每日播n-1次时的日销售量件an-1的基础上增加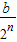 件.合同约定:每播一次企业需支付广告费2b元.
件.合同约定:每播一次企业需支付广告费2b元.