题目内容
下列各组向量中,可以作为基底的是 ( )
A. | B.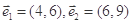 |
C. | D. |
D
解析考点:向量的几何表示.
专题:向量法.
分析:判断各个选项中的2个向量是否共线,共线的2个向量不能作为基底,不共线的2个向量可以作为基底.
解答:解:A、中的2个向量的坐标对应成比例, =
= ,所以,这2个向量是共线向量,故不能作为基底.
,所以,这2个向量是共线向量,故不能作为基底.
B、中的2个向量的坐标对应成比例, =
= ,所以,这2个向量是共线向量,故不能作为基底.
,所以,这2个向量是共线向量,故不能作为基底.
C中的2个向量的坐标对应成比例, =
= ,这2个向量是共线向量,故不能作为基底.
,这2个向量是共线向量,故不能作为基底.
D、中的2个向量的坐标对应不成比例, ≠
≠ ,所以,这2个向量不是共线向量,故可以作为基底.
,所以,这2个向量不是共线向量,故可以作为基底.
故选D.
点评:平面内任何2个不共线的向量都可以作为基底,当2个向量的坐标对应成比列时,这2个向量就是共线向量.

练习册系列答案
相关题目
已知 =(3,4),
=(3,4), =(5,12),
=(5,12), 与
与 则夹角的余弦为( )
则夹角的余弦为( )
A. | B. | C. | D.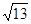 |
已知 是
是 的重心,
的重心, ,
, ,则
,则 的最小值是
的最小值是
A. | B. | C. | D.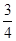 |
已知向量 ,则
,则 ( )
( )
A. | B. | C. -5 | D.5 |
已知O为 内任意的一点,若对任意
内任意的一点,若对任意 有
有 则
则 一定是
一定是
| A.直角三角形 | B.钝角三角形 | C.锐角三角形 | D.不能确定 |
4如图,正六边形ABCDEF中, ="( " )
="( " )
| A.0 | B. | C.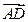 | D. |
已知向量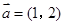 ,
, ,若向量
,若向量 ,则
,则 ( )
( )
A. | B. | C. | D.2 |
已知向量 不共线,
不共线, ,
, ,如果
,如果 ∥
∥ ,那么 ( )
,那么 ( )
A.k=1且 与 与 同向 同向 | B.k=1且 与 与 反向 反向 |
C.k=-1且 与 与 同向 同向 | D.k=-1且 与 与 反向 反向 |
 ,则k的值为 ( )
,则k的值为 ( )



