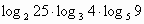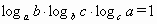题目内容
利用换底公式求log225•log34•log59的值.
分析:利用对数的运算法则和对数的换底公式即可得出.
解答:解:原式=log252•log322•log532
=2log25•2log32•2log53
=8log25•log32•log53
=8×
×
×
=8.
=2log25•2log32•2log53
=8log25•log32•log53
=8×
| lg5 |
| lg2 |
| lg2 |
| lg3 |
| lg3 |
| lg5 |
=8.
点评:本题考查了对数的运算法则和对数的换底公式,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
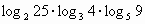 ;
;
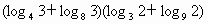 ;
;
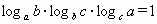 .(a>0,b>0,c>0,a≠1,b≠1,c≠1)
.(a>0,b>0,c>0,a≠1,b≠1,c≠1)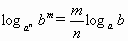 (其中
(其中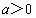 ,
,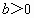 ,
,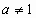 ,
,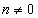 ).
).