题目内容
若三个互不相等的实数成等差数列,适当交换这三个数的位置后变成一个等比数列,则此等比数列的公比为 (写出一个即可).
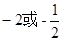
解析试题分析:设三个互不相等的实数为a-d,a,a+d,(d≠0),交换这三个数的位置后:
①若a是等比中项,则a2=(a-d)(a+d),解得d=0,不符合;②若a-d是等比中项,则(a-d)2=a(a+d),解得d=3a,此时三个数为a,-2a,4a,公比为-2或三个数为4a,-2a,a,公比为-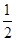 .③若a+d是等比中项,则同理得到公比为-2,或公比为-
.③若a+d是等比中项,则同理得到公比为-2,或公比为-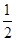 ,所以此等比数列的公比是-2或-
,所以此等比数列的公比是-2或-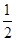
考点:本题考查了等差数列与等比数列的综合.
点评:解决等差数列、等比数列的问题时,常采用设出首项、公差、公比,利用基本量的方法列出方程组来解.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
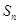 是等差数列{an}的前n项和,若
是等差数列{an}的前n项和,若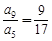 ,则
,则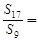 .
.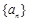 的前
的前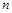 项和为
项和为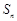 ,
,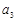 、
、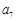 是方程
是方程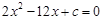 的两根,且
的两根,且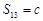 ,则数列
,则数列 .
.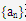 通项公式为
通项公式为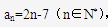 ,则
,则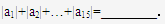
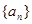 中,
中,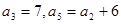 ,则
,则 .
. 的前
的前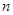 项和为
项和为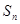 ,若
,若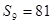 ,则
,则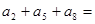
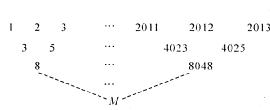
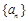 中,如果对任意的
中,如果对任意的 ,都有
,都有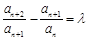 (
(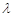 为常数),则称数列
为常数),则称数列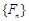 满足
满足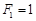 ,
,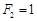 ,
,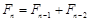 (
(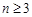 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列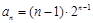 ,则数列
,则数列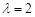 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若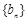 是等比数列,则数列
是等比数列,则数列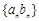 是比等差数列.
是比等差数列.