题目内容
离散型随机变量ξ的取值为x1,x2,x3,……,xi,…,且x1<x2<x3<…<xi<…,定义函数F(x)为:F(x)=P(ξ<x)=P(ξ=x1)+P(ξ=x2)+P(ξ=x3)+…+P(ξ=xi),其中xi<x,设某运动员投篮投中的概率为P=0.3,求一次投篮时投中次数的概率分布和函数F(x)。
答案:
解析:
解析:
解:这次投篮的投中次数是随机变量,设为ξ.它的取值为0和1,即x1=0,x2=1. ξ=0表示投中0次,即未投中,概率为1-0.3=0.7;ξ=1表示投中一次,即未投中,概率为0.3.故概率分布为
∵ 当x≤0时,, 当0<x≤1时, 当x>1时, ∴ 函数
|

练习册系列答案
相关题目
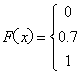
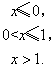
 为离散型随机变量,
为离散型随机变量, 的取值为
的取值为 ,则
,则 的取值为
的取值为  ,则
,则 ;
; ;
;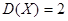 ,则
,则 .
.