题目内容
代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时 .
【答案】分析:将台风中心视为点B,进而可知AB的长度,过B作BC垂直正东线于点C,进而可知BC=200,AC=200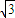 ,在BC线上取点D使得AD=350千米进而根据勾股定理求得DC,进而乘以2,再除以速度即是 A码头从受到台风影响的时间.
,在BC线上取点D使得AD=350千米进而根据勾股定理求得DC,进而乘以2,再除以速度即是 A码头从受到台风影响的时间.
解答:解:在距港口的A码头南偏东60°的400千米的海面
将台风中心视为点B,则AB=400 过B作BC垂直正东线于点C,则BC=200,AC=200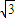
台风中心350千米的范围都会受到台风影响
所以在BC线上取点D使得AD=350千米
因为AC=200千米,AD=350千米∠DCA是直角
根据勾股定理
DC=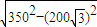 =50千米 因为350千米的范围内都会受到台风影响
=50千米 因为350千米的范围内都会受到台风影响
所以影响距离是50×2=100千米
T=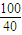 0=2.5(小时)
0=2.5(小时)
故答案为2.5小时.
点评:本题主要考查了解三角形的实际应用.考查了考生运用所学知识解决实际问题的能力.
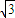 ,在BC线上取点D使得AD=350千米进而根据勾股定理求得DC,进而乘以2,再除以速度即是 A码头从受到台风影响的时间.
,在BC线上取点D使得AD=350千米进而根据勾股定理求得DC,进而乘以2,再除以速度即是 A码头从受到台风影响的时间.解答:解:在距港口的A码头南偏东60°的400千米的海面
将台风中心视为点B,则AB=400 过B作BC垂直正东线于点C,则BC=200,AC=200
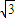
台风中心350千米的范围都会受到台风影响
所以在BC线上取点D使得AD=350千米
因为AC=200千米,AD=350千米∠DCA是直角
根据勾股定理
DC=
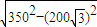 =50千米 因为350千米的范围内都会受到台风影响
=50千米 因为350千米的范围内都会受到台风影响所以影响距离是50×2=100千米
T=
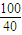 0=2.5(小时)
0=2.5(小时)故答案为2.5小时.
点评:本题主要考查了解三角形的实际应用.考查了考生运用所学知识解决实际问题的能力.

练习册系列答案
相关题目