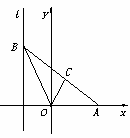题目内容
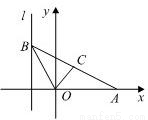
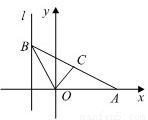
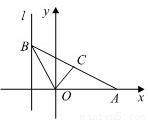
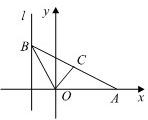 如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
分析:欲求点C的轨迹方程,设点C(x,y),只须求出其坐标x,y的关系式即可,由题意知点C到OA、OB距离相等得到一个关系式,化简即得点C的轨迹方程,最后对参数a进行讨论来判断轨迹是什么图形即可.
解答:解:依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.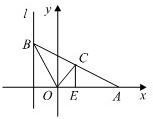
设点C(x,y),
则有0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等.
根据点到直线的距离公式得|y|=
.①
依题设,点C在直线AB上,故有y=-
(x-a).
由x-a≠0,得b=-
.②
将②式代入①式得y2[1+
]=[y-
]2,
整理得y2[(1-a)x2-2ax+(1+a)y2]=0.
若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);
若y=0,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式.
综上得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a)
因为a≠0,所以
+
=1(0≤x<a).
由此知,当0<a<1时,方程③表示椭圆弧段;
当a>1时,方程③表示双曲线一支的弧段;

设点C(x,y),
则有0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等.
根据点到直线的距离公式得|y|=
| |y+bx| | ||
|
依题设,点C在直线AB上,故有y=-
| b |
| 1+a |
由x-a≠0,得b=-
| (1+a)y |
| x-a |
将②式代入①式得y2[1+
| (1+a)2y2 |
| (x-a)2 |
| (1+a)xy |
| x-a |
整理得y2[(1-a)x2-2ax+(1+a)y2]=0.
若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);
若y=0,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式.
综上得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a)
因为a≠0,所以
(x-
| ||
(
|
| y2 | ||
|
由此知,当0<a<1时,方程③表示椭圆弧段;
当a>1时,方程③表示双曲线一支的弧段;
点评:本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目