题目内容
先后抛掷一枚骰子两次,将得到的点数分别记为a,b.
(Ⅰ)求点(a,b)在函数y=2x的图象上的概率;
(Ⅱ)将a,b,4的值分别作为三条线段长,求这三条线段能围成等腰三角形的概率.
(Ⅰ)求点(a,b)在函数y=2x的图象上的概率;
(Ⅱ)将a,b,4的值分别作为三条线段长,求这三条线段能围成等腰三角形的概率.
分析:(Ⅰ)点(a,b)在函数y=2x图象上包括 2中情况,由此求得点(a,b)在函数y=2x图象上的概率.
(Ⅱ)当a=1、2、3、4、5、6时,分别求出围成等腰三角形的个数,相加可得到所有的等腰三角形个数,而(a,b)的所有取值共36个,从而求得这三条线段能围成等腰三角形的概率.
(Ⅱ)当a=1、2、3、4、5、6时,分别求出围成等腰三角形的个数,相加可得到所有的等腰三角形个数,而(a,b)的所有取值共36个,从而求得这三条线段能围成等腰三角形的概率.
解答:解:先后抛掷一枚骰子两次,基本事件总数为36.…(2分)
(Ⅰ)记“点(a,b)在函数y=2x的图象上”为事件B,包含(1,2),(2,4)两个基本事件,
所以P(B)=
=
答:点(a,b)在函数y=2x的图象上的概率为
.…(8分)
(Ⅱ)记“a,b,4为边能围成等腰三角形”为事件C,它包括14个基本事件.…(12分)
所以P(C)=
=
答:这三条线段能围成等腰三角形的概率为
.…(14分)
(Ⅰ)记“点(a,b)在函数y=2x的图象上”为事件B,包含(1,2),(2,4)两个基本事件,
所以P(B)=
| 2 |
| 36 |
| 1 |
| 18 |
答:点(a,b)在函数y=2x的图象上的概率为
| 1 |
| 18 |
(Ⅱ)记“a,b,4为边能围成等腰三角形”为事件C,它包括14个基本事件.…(12分)
所以P(C)=
| 14 |
| 36 |
| 7 |
| 18 |
答:这三条线段能围成等腰三角形的概率为
| 7 |
| 18 |
点评:本题主要考查等可能事件的概率,古典概型,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
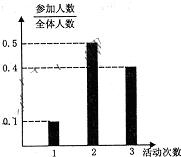 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. ,
, 。
。 的概率;
的概率; 在函数
在函数 图像上的概率;
图像上的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。