题目内容
已知函数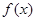 的图像关于
的图像关于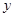 轴对称,并且是[0,+
轴对称,并且是[0,+ 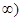 上的减函数,若
上的减函数,若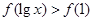 , 则实数
, 则实数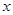 的取值范围是 ( )
的取值范围是 ( )
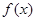 的图像关于
的图像关于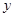 轴对称,并且是[0,+
轴对称,并且是[0,+ 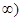 上的减函数,若
上的减函数,若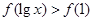 , 则实数
, 则实数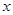 的取值范围是 ( )
的取值范围是 ( )A. | B. | C. | D. |
C
分析:由题意可得函数f(x)在(-∞,0]上单调递增,且f(1)=f(-1),故由f(lgx)>f(1),可得-1<lgx<1,由此解得实数x的取值范围.
解答:解:∵函数f(x)的图象关于y轴对称,并且是[0,+∞)上的减函数,故在(-∞,0]上单调递增,且f(1)=f(-1).
故由f(lgx)>f(1),可得-1<lgx<1,解得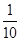 <x<10,
<x<10,
故选C.
点评:本题主要考查对数函数的单调性和特殊点,函数的单调性和奇偶性的应用,属于中档题.
解答:解:∵函数f(x)的图象关于y轴对称,并且是[0,+∞)上的减函数,故在(-∞,0]上单调递增,且f(1)=f(-1).
故由f(lgx)>f(1),可得-1<lgx<1,解得
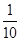 <x<10,
<x<10,故选C.
点评:本题主要考查对数函数的单调性和特殊点,函数的单调性和奇偶性的应用,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
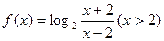 .
.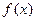 在
在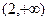 为减函数;
为减函数;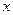 的不等式
的不等式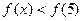 .
.
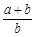


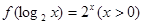 ,则
,则 的值是( )
的值是( )



 (
( ),对于任意的正实数x,y,都有
),对于任意的正实数x,y,都有



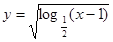 的定义域为 .
的定义域为 . ,则其定义域为: 。
,则其定义域为: 。 B.
B.
 D.
D.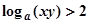
 ”,“=”,“>”之一)
”,“=”,“>”之一)