题目内容
设命题P:x1,x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立,命题Q:不等式|x-2m|-|x|>1(m>0)有解,若P且Q为真,试求实数m的取值范围.
【答案】分析:由方程的根与系数关系可得,x1+x2=a,x1x2=-2,而|x1-x2|=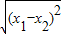 =
=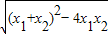 代入结合a得范围可求|x1-x2|的最大值,结合已知可得|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可,从而可求P对应的m得范围;再由不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1,从而可求Q所对应的m的范围,由P且Q为真可知P,Q都为真命题,即可求
代入结合a得范围可求|x1-x2|的最大值,结合已知可得|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可,从而可求P对应的m得范围;再由不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1,从而可求Q所对应的m的范围,由P且Q为真可知P,Q都为真命题,即可求
解答:解:∵x1,x2是方程x2-ax-2=0的两个实根
∴x1+x2=a,x1x2=-2
∴|x1-x2|=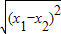 =
=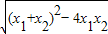 =
=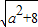
当a∈[-1,1]时,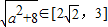
∵不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立
则只要|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可
∴|m2-5m-3|≥3
∴m2-5m-3≥3或m2-5m-3≤-3
即m2-5m-6≥0或m2-5m≤0
解不等式可m2-5m-6≥0得,m≥6或m≤-1
解不等式m2-5m≤0得,0≤m≤5
综上可得,P:m≥6或m≤-1或0≤m≤5
∵不等式|x-2m|-|x|>1(m>0)有解
令f(x)=|x-2m|-|x|=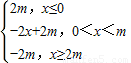 ,
,
结合该函数的性质可知,函数的最大值为2m,最小值为-2m
若使得不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1即2m>1即可
Q:m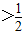
∵P且Q为真
∴P,Q都为真命题
∴
∴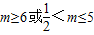
点评:本题目主要考查了复合命题的真假判断的应用,解题得关键是熟练应用函数的知识准确求出命题P,Q为真时的m的取值范围.
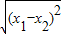 =
=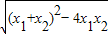 代入结合a得范围可求|x1-x2|的最大值,结合已知可得|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可,从而可求P对应的m得范围;再由不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1,从而可求Q所对应的m的范围,由P且Q为真可知P,Q都为真命题,即可求
代入结合a得范围可求|x1-x2|的最大值,结合已知可得|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可,从而可求P对应的m得范围;再由不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1,从而可求Q所对应的m的范围,由P且Q为真可知P,Q都为真命题,即可求解答:解:∵x1,x2是方程x2-ax-2=0的两个实根
∴x1+x2=a,x1x2=-2
∴|x1-x2|=
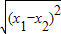 =
=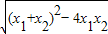 =
=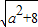
当a∈[-1,1]时,
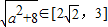
∵不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立
则只要|m2-5m-3|≥|x1-x2|max在a∈[-1,1]成立即可
∴|m2-5m-3|≥3
∴m2-5m-3≥3或m2-5m-3≤-3
即m2-5m-6≥0或m2-5m≤0
解不等式可m2-5m-6≥0得,m≥6或m≤-1
解不等式m2-5m≤0得,0≤m≤5
综上可得,P:m≥6或m≤-1或0≤m≤5
∵不等式|x-2m|-|x|>1(m>0)有解
令f(x)=|x-2m|-|x|=
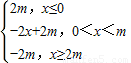 ,
,结合该函数的性质可知,函数的最大值为2m,最小值为-2m
若使得不等式|x-2m|-|x|>1(m>0)有解,则只要f(x)max>1即2m>1即可
Q:m
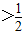
∵P且Q为真
∴P,Q都为真命题
∴

∴
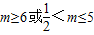
点评:本题目主要考查了复合命题的真假判断的应用,解题得关键是熟练应用函数的知识准确求出命题P,Q为真时的m的取值范围.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目