题目内容
甲乙两地相距400千米,汽车从甲地匀速行驶到乙地,速度不得超过100千米/小时,已知该汽车每小时的运输成本P(元)关于速度v(千米/小时)的函数关系是P=| 1 |
| 19200 |
| 1 |
| 160 |
(1)求全程运输成本Q(元)关于速度v的函数关系式;
(2)为使全程运输成本最少,汽车应以多少速度行驶?并求此时运输成本的最小值.
分析:(1)因为每小时的运输成本p关于v的解析式知道,要求全程运输成本只需要求出全程用的时间就行了,根据时间=
求得.
(2)求出Q的导数,令其为零,求出v1.讨论在区间(0,100)上,(0,v1)时Q'<0函数是减函数;(v1,100)时Q'>0函数是增函数;得到此函数Q有极小值,即最小值.就是全程运输成本有最小值.
| 路程 |
| 速度 |
(2)求出Q的导数,令其为零,求出v1.讨论在区间(0,100)上,(0,v1)时Q'<0函数是减函数;(v1,100)时Q'>0函数是增函数;得到此函数Q有极小值,即最小值.就是全程运输成本有最小值.
解答:解:(1)Q=P•
=(
v4-
v3+15v)•
=(
v3-
v2+15)•400
=
-
v2+6000(0<v≤100).
(2)Q′=
-5v,
令Q′=0,则v=0(舍去)或v=80,
当0<v<80时,Q′<0.
当80<v≤100时,Q′>0.
∴v=80时,全程运输成本取得极小值,即最小值.
从而Qmin=Q(80)=
元.
| 400 |
| v |
| 1 |
| 19200 |
| 1 |
| 160 |
| 400 |
| v |
=(
| 1 |
| 19200 |
| 1 |
| 160 |
=
| v3 |
| 48 |
| 5 |
| 2 |
(2)Q′=
| v2 |
| 16 |
令Q′=0,则v=0(舍去)或v=80,
当0<v<80时,Q′<0.
当80<v≤100时,Q′>0.
∴v=80时,全程运输成本取得极小值,即最小值.
从而Qmin=Q(80)=
| 2000 |
| 3 |
点评:考查学生列函数解析式并且知道导数等于零是函数取得极值的必要条件,利用导数求闭区间上的最值.

练习册系列答案
相关题目
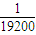 v4-
v4-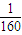 v3+15v,
v3+15v,