题目内容
将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y= .据此类推可求得双曲线
.据此类推可求得双曲线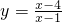 的焦距为
的焦距为
- A.2

- B.2

- C.4
- D.4

D
分析:由于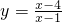 =
=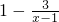 ,双曲线
,双曲线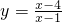 的图象可由
的图象可由 进行变换而得,从而得到双曲线
进行变换而得,从而得到双曲线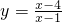 的图象与双曲线
的图象与双曲线 的图象全等,它们的焦距相同,又根据题意得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线
的图象全等,它们的焦距相同,又根据题意得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线 .
.
故只须求出双曲线x2-y2=6的焦距即可.
解答:由于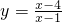 =
=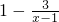 ,双曲线
,双曲线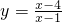 的图象可由
的图象可由 进行形状不变的变换而得,
进行形状不变的变换而得,
∴双曲线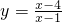 的图象与双曲线
的图象与双曲线 的图象全等,它们的焦距相同,
的图象全等,它们的焦距相同,
根据题意:“将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y= .“
.“
类比可得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线 .
.
而双曲线x2-y2=6的a=b= ,c=2
,c=2 ,
,
∴焦距为2c=4 ,
,
故选D.
点评:本小题主要考查旋转变换、双曲线的简单性质等基础知识,考查运算求解能力,考查分析问题和解决问题的能力.属于基础题.
分析:由于
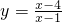 =
=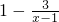 ,双曲线
,双曲线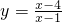 的图象可由
的图象可由 进行变换而得,从而得到双曲线
进行变换而得,从而得到双曲线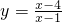 的图象与双曲线
的图象与双曲线 的图象全等,它们的焦距相同,又根据题意得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线
的图象全等,它们的焦距相同,又根据题意得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线 .
.故只须求出双曲线x2-y2=6的焦距即可.
解答:由于
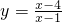 =
=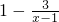 ,双曲线
,双曲线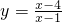 的图象可由
的图象可由 进行形状不变的变换而得,
进行形状不变的变换而得,∴双曲线
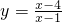 的图象与双曲线
的图象与双曲线 的图象全等,它们的焦距相同,
的图象全等,它们的焦距相同,根据题意:“将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y=
 .“
.“类比可得:将双曲线x2-y2=6绕原点逆时针旋转45°后可得到双曲线
 .
.而双曲线x2-y2=6的a=b=
 ,c=2
,c=2 ,
,∴焦距为2c=4
 ,
,故选D.
点评:本小题主要考查旋转变换、双曲线的简单性质等基础知识,考查运算求解能力,考查分析问题和解决问题的能力.属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分. .据此类推可求得双曲线
.据此类推可求得双曲线 的焦距为( )
的焦距为( )

