Question

若方程7x²-（k+13）x+k²-k-2=0的两根分别在（0，1）和（1，2）内，求k的取值范围．

Answer 1

分析：设出方程相应的二次函数，据方程的根的分布情况画出二次函数的图象；结合图，令f（0）＞0，f（1）＜0，f（2）＞0；解不等式组求出k的范围．

解答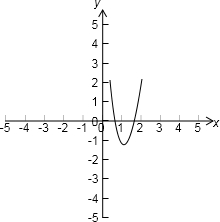：解：设f（x）=7x²-（k+13）x+k²-k-2
∵方程7x²-（k+13）x+k²-k-2=0的两根分别在（0，1）和（1，2）内
∴f（x）的图象如下：
所以

f(0)=k2-k-2＞0 f(1)=k2-2k-8＜0 f(2)=k2-3k＞0

解得-2＜k＜-1或3＜k＜4
所以k的范围为（-2，-1）∪（3，4）

点评：本题考查解决二次方程的根的分布常画出相应的二次函数的图象，从开口方向、判别式、区间的端点值的正负上加以限制．