题目内容
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所:
每张钢板的面积:第一种为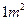 ,第二种为
,第二种为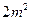 。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
| 类型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
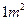 ,第二种为
,第二种为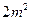 。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小.
设需截第一种钢板工张x张,第二种钢板y张,所用钢板面积为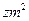 ,(1分)
,(1分)
 则有
则有 (5分)
(5分)
作出可行域(如图) (8分)
目标函数为: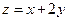
作出一组平行直线 (t为参数).由
(t为参数).由 得
得 (11分)
(11分)
由于点 不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使z最小,且
不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使z最小,且 (13分)
(13分)
答:应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小. (14分)
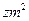 ,(1分)
,(1分) 则有
则有 (5分)
(5分)
作出可行域(如图) (8分)
目标函数为:
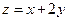
作出一组平行直线
 (t为参数).由
(t为参数).由 得
得 (11分)
(11分)由于点
 不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使z最小,且
不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使z最小,且 (13分)
(13分)答:应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小. (14分)

练习册系列答案
相关题目
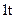 成本1 000元,运费500元,可得产品90kg,若采用乙种原料
成本1 000元,运费500元,可得产品90kg,若采用乙种原料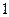 t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?
t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?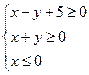 表示的平面区域的面积为________
表示的平面区域的面积为________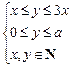 的有序数对
的有序数对 为“和谐格点”,则当
为“和谐格点”,则当 时,和谐格点的个数是 .
时,和谐格点的个数是 . ,则
,则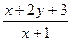 的取值范围是( )
的取值范围是( )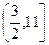
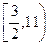
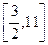

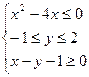 表示的平面区域为M,
表示的平面区域为M,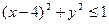 表示的平面区域为N,现随机向区域M内抛一点,则该点落在平面区域N内的概率是 。
表示的平面区域为N,现随机向区域M内抛一点,则该点落在平面区域N内的概率是 。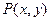 的坐标满足条件
的坐标满足条件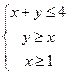 ,点
,点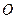 为坐标原点,那么
为坐标原点,那么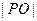 的最大值等于_______,最小值等于____________.
的最大值等于_______,最小值等于____________.