题目内容
在平面几何中,有这样一个定理:过三角形的内心作一直线,将三角形分成的两部分的周长比等于其面积比.请你类比写出在立体几何中,有关四面体的相似性质: .
过四面体的内切球的球心作截面交三条棱于三点,则分成的两部分体积之比等于表面积之比.
解析试题分析:设四面体 的内切球的球心为
的内切球的球心为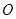 ,过
,过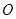 作截面
作截面 交三条棱于点
交三条棱于点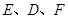 ,记内切圆半径为
,记内切圆半径为 ,则
,则 也表示点
也表示点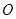 到各面的距离,利用体积的“割补法”知:
到各面的距离,利用体积的“割补法”知:
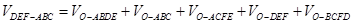

从而 .
.
考点:类比问题.

练习册系列答案
相关题目
题目内容
在平面几何中,有这样一个定理:过三角形的内心作一直线,将三角形分成的两部分的周长比等于其面积比.请你类比写出在立体几何中,有关四面体的相似性质: .
过四面体的内切球的球心作截面交三条棱于三点,则分成的两部分体积之比等于表面积之比.
解析试题分析:设四面体 的内切球的球心为
的内切球的球心为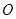 ,过
,过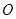 作截面
作截面 交三条棱于点
交三条棱于点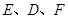 ,记内切圆半径为
,记内切圆半径为 ,则
,则 也表示点
也表示点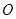 到各面的距离,利用体积的“割补法”知:
到各面的距离,利用体积的“割补法”知:
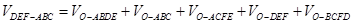

从而 .
.
考点:类比问题.
