题目内容
已知点F是双曲线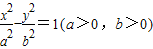 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )A.(1,2)
B.(1,+∞)
C.
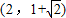
D.
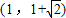
【答案】分析:利用双曲线的对称性及锐角三角形∠ACF<45°得到AF<CF,求出A的坐标;求出AF,CF得到关于a,b,c的不等式,求出离心率的范围.
解答:解:∵△ABC是锐角三角形
∴∠ACB为锐角
∵双曲线关于x轴对称,且直线AB垂直x轴
∴∠ACF=∠BCF<45°
∴AF<CF
∵F为右焦点,设其坐标为(c,0)
所以A(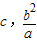 )
)
所以AF=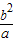 ,CF=a+c
,CF=a+c
∴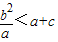 即c2-ac-2a2<0
即c2-ac-2a2<0
解得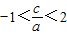
双曲线的离心率的范围是(1,2)
故选A.
点评:本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率问题就是研究三参数a,b,c的关系.
解答:解:∵△ABC是锐角三角形
∴∠ACB为锐角
∵双曲线关于x轴对称,且直线AB垂直x轴
∴∠ACF=∠BCF<45°
∴AF<CF
∵F为右焦点,设其坐标为(c,0)
所以A(
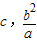 )
)所以AF=
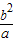 ,CF=a+c
,CF=a+c∴
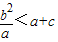 即c2-ac-2a2<0
即c2-ac-2a2<0解得
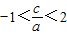
双曲线的离心率的范围是(1,2)
故选A.
点评:本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率问题就是研究三参数a,b,c的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
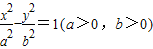 的右焦点,若过点F且倾斜角为60°的直线与双曲线的右支有两个交点,则该双曲线的离心率e的取值范围是( )
的右焦点,若过点F且倾斜角为60°的直线与双曲线的右支有两个交点,则该双曲线的离心率e的取值范围是( )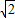 )
)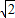 )
)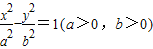 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
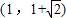
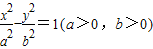 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )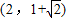
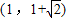
 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
