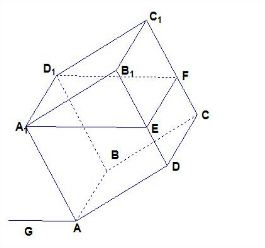
题目内容
 一个正方体形状的铁桶ABCD-A1B1C1D1的内壁的体积为V,里面装有体积为
一个正方体形状的铁桶ABCD-A1B1C1D1的内壁的体积为V,里面装有体积为| 2 | 3 |
分析:解决本题的关键是要抓住倾斜前后的体积不变去计算,计算时要注意有水部分的几何体的形状由先前的长方体变成了后来的四棱台,计算棱台的体积需要知道上下底面的面积,故可设ED=x,由体积关系进一步得到:x与a的关系;通过思考、观察可知:由等角定理可知:∠B1EA=∠A1AG,可以证明:∠A1AG即为平面ABB1A1与地面所成的二面角的平面角,所以在Rt△A1B1E中,可以求得∠B1EA的余弦值的大小,即∠A1AG的余弦值的大小,此值即为所求.
解答:解:如图所示,四边形A1EFD1所在的平面即为当铁桶中的水刚好要留出时的水面,
设正方体的棱长为a,ED=x,
则S四边形A1ABD1=a2,S四边形EDCF=ax,v=a3
∴V四棱台EFCD-A1ABD1=
•a•(a2+ax+
)=
a3
∴x+
-a=0
∴x=(
)2a
∴B1E=
a
又∵A1B1=a,
∴A1E=
a
∴cos∠B1EA=
=
又∵B1E∥A1A,A1E∥GA,
∴∠B1EA=∠A1AG
又∵A1A⊥AB,GA⊥AB,
∴∠A1AG即为平面ABB1A1与地面所成的二面角的平面角
又∵cos∠A1AG=
∴所求倾斜角的余弦值为
故答案为:
设正方体的棱长为a,ED=x,
则S四边形A1ABD1=a2,S四边形EDCF=ax,v=a3
∴V四棱台EFCD-A1ABD1=
| 1 |
| 3 |
| a2•ax |
| 2 |
| 3 |
∴x+
| ax |
∴x=(
| ||
| 2 |
∴B1E=
| ||
| 2 |
又∵A1B1=a,
∴A1E=
5-
| ||
| 2 |
∴cos∠B1EA=
| B1E |
| A1E |
| ||
| 5 |
又∵B1E∥A1A,A1E∥GA,
∴∠B1EA=∠A1AG
又∵A1A⊥AB,GA⊥AB,
∴∠A1AG即为平面ABB1A1与地面所成的二面角的平面角
又∵cos∠A1AG=
| ||
| 5 |
∴所求倾斜角的余弦值为
| ||
| 5 |
故答案为:
| ||
| 5 |

点评:本小题主要考查棱柱、棱锥、棱台的结构特征、体积计算,二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
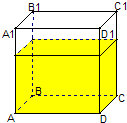 一个正方体形状的无盖铁桶ABCD-A1B1C1D1的容积是V,里面装有体积为
一个正方体形状的无盖铁桶ABCD-A1B1C1D1的容积是V,里面装有体积为 V的水,放在水平的地面上(如图所示).现以顶点A为支撑点,将铁桶倾斜,当铁桶中的水刚好要从顶点A1处流出时,棱AA1与地面所成角的余弦值为 .
V的水,放在水平的地面上(如图所示).现以顶点A为支撑点,将铁桶倾斜,当铁桶中的水刚好要从顶点A1处流出时,棱AA1与地面所成角的余弦值为 .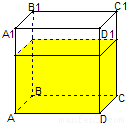
 V的水,放在水平地面上(如图所示),现沿棱AB将铁桶倾斜,当铁桶中的水刚好要留出时,倾斜角(平面ABB1A1与地面所成的二面角)的余弦值为 .
V的水,放在水平地面上(如图所示),现沿棱AB将铁桶倾斜,当铁桶中的水刚好要留出时,倾斜角(平面ABB1A1与地面所成的二面角)的余弦值为 .