Question

点P(2,2)在抛物线C:y²=2px(p＞0)上,抛物线C上动点A、B不同于原点O.

(1)求抛物线的方程.

(2)若·=0,求证：直线AB过定点.

(3)若直线AB恒过定点M(6,0),求∠AOB的最小值.

Answer 1

答案：(1)解:∵P(2,2)在抛物线y²=2px上,∴4=2p·2.∴2p=2.∴抛物线方程为y²=2x.

(2)证明:设A(x₁,y₁),B(x₂,y₂),则·=x₁x₂+y₁y₂且y₁²=2x₁,y₂²=2x₂.

∵·=0,∴·+y₁y₂=0.∴y₁y₂(y₁y₂+4)=0.∵y₁y₂≠0,∴y₁y₂=-4.

k_AB=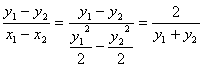.∴直线AB的方程为y-y₁=(x-x₁),

即(y₁+y₂)y-y₁²-y₁y₂=2x-2x₁.又y₁²=2x₁,y₁y₂=-4,∴(y₁+y₂）y=2(x-2).∴直线AB过定点(2,0).

(3)解:k_OA==,k_OB=，不妨设y₁＞0,y₂＜0.

则∠AOB为直线OB到OA的角，∴tan∠AOB=.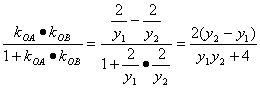

∵直线AB过点M(6,0),∴设直线AB的方程为x=ay+6,代入y²=2x,

得y²-2ay-12=0,得y₁y₂=-12.10分tan∠AOB=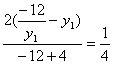(y₁+)≥·2=3(当且仅当y₁=y₂=2,取等号),∴∠AOB的最小值为.