题目内容
设集合A={x|-1≤x≤2},B={x|x2-4x>0,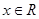 },则A∩(CRB)=( )
},则A∩(CRB)=( )
A. B.[0,2] C.[1,4] D.[0,4]
B.[0,2] C.[1,4] D.[0,4]
B
解析试题分析:因为,B={x|x2-4x>0,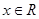 }=
}= 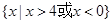 ,
,
所以,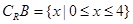 ,A∩(CRB)={x|-1≤x≤2}
,A∩(CRB)={x|-1≤x≤2}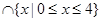 =[0,2],
=[0,2],
故选B。
考点:简单不等式的解法,集合的运算。
点评:简单题,为进行集合的运算,需要首先确定集合中的元素。当实数范围较复杂时,可借助于数轴处理。

练习册系列答案
相关题目
已知集合 的非空子集
的非空子集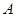 具有性质
具有性质 :当
:当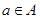 时,必有
时,必有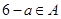 .则具有性质
.则具有性质 的集合
的集合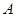 的个数是 ( )
的个数是 ( )
A.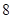 | B.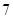 | C.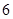 | D. |
若 则
则 ( )
( )
| A.(-2,2) | B.(-2,0) | C.(0,2) | D.(-2,-1) |
设集合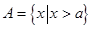 ,集合
,集合 ,若
,若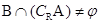 ,则实数
,则实数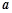 的取值范围是( )
的取值范围是( )
A. | B. | C.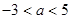 | D. |
对于数集A, B, 定义A+B="{x|x=a+b," a∈A, b∈B), A÷B={x|x=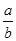 ,
, 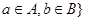 , 若集合A="{1," 2}, 则集 合(A+A)÷A中所有元素之和为( )
, 若集合A="{1," 2}, 则集 合(A+A)÷A中所有元素之和为( )
A.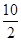 B.
B.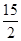 C.
C.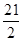 D.
D.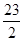
设集合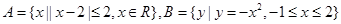 ,则
,则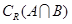 等于 ( )
等于 ( )
| A.R | B. | C.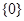 | D.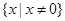 |
已知集合 ,
, ,则
,则 =
=
A. | B.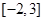 | C. | D.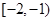 |
已知集合
A. | B. | C. | D. |