题目内容
1、已知集合A,B都是非空集合,则“x∈(A∪B)”是“x∈A且x∈B”的( )
分析:验证“x∈(A∪B)”不能推出“x∈A且x∈B”,举反例即可,“x∈A且x∈B”能推出“x∈(A∪B)”,根据并集的定义即可,故得到结论.
解答:解:“x∈(A∪B)”不能推出“x∈A且x∈B”,
如A={1,2},B={2,3},则A∪B={1,2,3},A∩B={2},
显然1∈A∪B,但1∉A∩B,因此“x∈(A∪B)”不能推出“x∈A且x∈B”;
“x∈A且x∈B”能推出“x∈(A∪B)”,
根据A∪B的定义即可求得结果,
故“x∈(A∪B)”是“x∈A且x∈B”的必要不充分条件,
故选B.
如A={1,2},B={2,3},则A∪B={1,2,3},A∩B={2},
显然1∈A∪B,但1∉A∩B,因此“x∈(A∪B)”不能推出“x∈A且x∈B”;
“x∈A且x∈B”能推出“x∈(A∪B)”,
根据A∪B的定义即可求得结果,
故“x∈(A∪B)”是“x∈A且x∈B”的必要不充分条件,
故选B.
点评:此题是基础题.考查充分必要条件和集合的交集并集的定义,以及学生对基本概念的理解程度.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
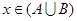 ”是“
”是“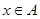 且
且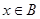 ”的
”的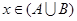 ”是“
”是“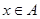 且
且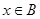 ”的( )
”的( )