题目内容
对于在[a,b]上有意义的两个函数f(x)与g(x),如果对任意的x∈[a,b],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[a,b]上是接近的,否则称f(x)与g(x)在[a,b]上是非接近的.现在有两个函数f(x)=logt(x-3t)与g(x)=logt(
)(t>0且t≠1),现给定区间[t+2,t+3].
(1)若t=
,判断f(x)与g(x)是否在给定区间上接近;
(2)若f(x)与g(x)在给定区间[t+2,t+3]上都有意义,求t的取值范围;
(3)讨论f(x)与g(x)在给定区间[t+2,t+3]上是否是接近的.
| 1 |
| x-t |
(1)若t=
| 1 |
| 2 |
(2)若f(x)与g(x)在给定区间[t+2,t+3]上都有意义,求t的取值范围;
(3)讨论f(x)与g(x)在给定区间[t+2,t+3]上是否是接近的.
(1)当t=
时,f(x)-g(x)=logt[(x-
)(x-
)]=logt[(x-1)2-
]
令h(x)=logt[(x-1)2-
]
当x∈[
,
]时,h(x)∈[log6,-1]
即|f(x)-g(x)|≥1,
f(x)与g(x)是否在给定区间上是非接近的
(2)由题意知,t>0且t≠1,t+2-3t>0,t+2-t>0
∴0<t<1
(3)∵|f(x)-g(x)|=|logt(x2-4tx+3t2)|
假设f(x)与g(x)在给定区间[t+2,t+3]上是接近的,
则有|logt(x2-4tx+3t2)|≤1∴-1≤logt(x2-4tx+3t2)≤1
令G(x)=logt(x2-4tx+3t2),当∴0<t<1时,[t+2,t+3]在x=2t的右侧,
即G(x)=logt(x2-4tx+3t2),在[t+2,t+3]上为减函数,
∴G(x)max=logt(4-4t),
∴G(x)min=logt(9-6t)
所以由(*)式可得{0<t<1logt(4-4t)≤1logt(9-6t)≥-1,解得
0<t≤
因此,当0<t≤
时,f(x)与g(x)在给定区间[t+2,t+3]上是接近的;当t>
时,
f(x)与g(x)在给定区间[t+2,t+3]上是非接近的.…(14分)
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
令h(x)=logt[(x-1)2-
| 1 |
| 4 |
当x∈[
| 5 |
| 2 |
| 7 |
| 2 |
即|f(x)-g(x)|≥1,
f(x)与g(x)是否在给定区间上是非接近的
(2)由题意知,t>0且t≠1,t+2-3t>0,t+2-t>0
∴0<t<1
(3)∵|f(x)-g(x)|=|logt(x2-4tx+3t2)|
假设f(x)与g(x)在给定区间[t+2,t+3]上是接近的,
则有|logt(x2-4tx+3t2)|≤1∴-1≤logt(x2-4tx+3t2)≤1
令G(x)=logt(x2-4tx+3t2),当∴0<t<1时,[t+2,t+3]在x=2t的右侧,
即G(x)=logt(x2-4tx+3t2),在[t+2,t+3]上为减函数,
∴G(x)max=logt(4-4t),
∴G(x)min=logt(9-6t)
所以由(*)式可得{0<t<1logt(4-4t)≤1logt(9-6t)≥-1,解得
0<t≤
9-
| ||
| 12 |
因此,当0<t≤
9-
| ||
| 12 |
9-
| ||
| 12 |
f(x)与g(x)在给定区间[t+2,t+3]上是非接近的.…(14分)

练习册系列答案
相关题目
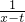 )(t>0且t≠1),现给定区间[t+2,t+3].
)(t>0且t≠1),现给定区间[t+2,t+3]. ,判断f(x)与g(x)是否在给定区间上接近;
,判断f(x)与g(x)是否在给定区间上接近;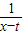 )(t>0且t≠1),现给定区间[t+2,t+3].
)(t>0且t≠1),现给定区间[t+2,t+3]. ,判断f(x)与g(x)是否在给定区间上接近;
,判断f(x)与g(x)是否在给定区间上接近;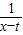 )(t>0且t≠1),现给定区间[t+2,t+3].
)(t>0且t≠1),现给定区间[t+2,t+3]. ,判断f(x)与g(x)是否在给定区间上接近;
,判断f(x)与g(x)是否在给定区间上接近;