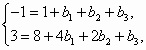题目内容
由等式x3+a1x2+a2x+a3=(x+1)3+b1(x+1)2+b2(x+1)+b3,定义一个映射:f(a1,a2,a3)=(b1,b2,b3),则f(2,1,-1)等于
[ ]
A.
(-1,0,-1)
B.
(-1,-1,0)
C.
(-1,0,1)
D.
(-1,1,0)
答案:A
解析:
解析:
|
由题意知x3+2x2+x-1=(x+1)3+b1(x+1)2+b2(x+1)+b3, 令x=-1,得-1=b3,即b3=-1; 再令x=0与x=1,得 解得b1=-1,b2=0,故选A. |

练习册系列答案
相关题目
由等式x3+a1x2+a2x+a3=(x+1)3+b1(x+1)2+b2(x+1)+b3,定义一个映射:f(a1,a2,a3)=(b1,b2,b3),则f(2,1,-1)等于( )
| A、(-1,0,-1) | B、(-1,-1,0) | C、(-1,0,1) | D、(-1,1,0) |