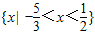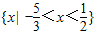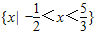Question

设S={x|1-2x＞0}T={x|3x+5＞0}，则S∩T=（　　）

• A．φ
• B．{x| x＞

  1

  2

  }
• C．{x| -

  5

  3

  ＜x＜

  1

  2

  }
• D．{x| -

  1

  2

  ＜x＜

  5

  3

  }

Answer 1

分析：分别求出两集合中不等式的解集，确定出两集合，找出两解集的公共部分，即可确定出两集合的交集．

解答：解：由集合S中的不等式1-2x＞0，解得：x＜

1

2

，
∴S={x|x＜

1

2

}，
由集合T中的不等式3x+5＞0，解得：x＞-

5

3

，
∴T={x|x＞-

5

3

}，
则S∩T={x|-

5

3

＜x＜

1

2

}．
故选C

点评：此题属于以一元一次不等式的解法为平台，考查了交集及其运算，熟练掌握交集的定义是解本题的关键．