题目内容
求函数y=sin(x+| π |
| 6 |
| π |
| 6 |
分析:利用两角和差的三角公式化简函数解析式并换元得 y=f(t)=-t2+at+
,对称轴为t=
,分
≤-1、-1<
<1、
≥1三种情况,利用函数的单调性分别求出最大值.
| 3 |
| 4 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:解:函数y=sin(x+
)sin(x-
)+acosx=-cos2x+acosx+
,
设t=cosx,则f(t)=-t2+at+
,对称轴为t=
.
(1)当
≤-1,即a≤-2时,函数在[-1,1]上单调递减,∴ymax=f(t)max=f(-1)=-a-
.
(2)当-1<
<1,即-2<a<2时,函数在[-1,1]先增后减,∴ymax=f(t)max=f(
)=
+
.
(3)当
≥1,即a≥2时,函数在[-1,1]上单调递增,∴ymax=f(t)max=f(1)=a-
.
综上所述,当a≤-2时,∴ymax=-a-
;
当-2<a<2时,∴ymax=
+
;
当a≥2时,∴ymax=a-
.
| π |
| 6 |
| π |
| 6 |
| 3 |
| 4 |
设t=cosx,则f(t)=-t2+at+
| 3 |
| 4 |
| a |
| 2 |
(1)当
| a |
| 2 |
| 1 |
| 4 |
(2)当-1<
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| 3 |
| 4 |
(3)当
| a |
| 2 |
| 1 |
| 4 |
综上所述,当a≤-2时,∴ymax=-a-
| 1 |
| 4 |
当-2<a<2时,∴ymax=
| a2 |
| 4 |
| 3 |
| 4 |
当a≥2时,∴ymax=a-
| 1 |
| 4 |
点评:本题考查二次函数的性质,余弦函数的值域,体现了分类讨论的数学思想,分类讨论是解题的难点.

练习册系列答案
相关题目
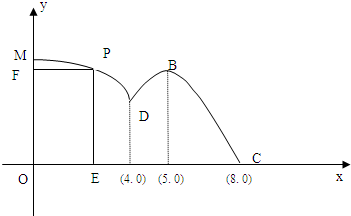
 ),x∈[4,8]时的图象,图象的最高点为
),x∈[4,8]时的图象,图象的最高点为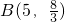

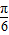 )sin(x-
)sin(x-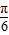 )+acosx的最大值.(其中a为定值)
)+acosx的最大值.(其中a为定值) ),x∈[4,8]时的图象,图象的最高点为
),x∈[4,8]时的图象,图象的最高点为
