题目内容
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)成为平面斜坐标系. 在平面斜坐标系 中,
中, (其中
(其中 ,
, 分别是斜坐标系
分别是斜坐标系 轴,
轴, 轴正方向上的单位向量,
轴正方向上的单位向量, ,
, ,
, 为坐标系原点),则有序数对
为坐标系原点),则有序数对 称为点
称为点 的斜坐标,在平面斜坐标系
的斜坐标,在平面斜坐标系 中,
中, ,点
,点 的斜坐标为
的斜坐标为 ,则以点
,则以点 位圆心,2为半径的圆在斜坐标系
位圆心,2为半径的圆在斜坐标系 中的方程为( )
中的方程为( )
A. | B. |
C. | D. |
C
解析试题分析:设在斜坐标系下,圆上的点 ,则
,则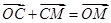 ,
,
∴ ,由
,由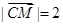 ,
, ,
,
∴ ,整理得
,整理得 ,故选C.
,故选C.
考点:平面向量的坐标运算,圆的性质.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
已知平面向量 ,
, ,则向量
,则向量 ( )
( )
A. | B.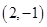 | C. | D. |
在 中,
中, 是
是 边的中点,角
边的中点,角 的对边分别是
的对边分别是 ,若
,若 ,则
,则 的形状为( )
的形状为( )
| A.直角三角形 | B.钝角三角形 |
| C.等边三角形 | D.等腰三角形但不是等边三角形 |
已知 ,
, ,
, ,若
,若 与
与 共线,则
共线,则 等于 ( )
等于 ( )
| A.5 | B.1 | C. | D. |
若平面向量
 与
与 的夹角是
的夹角是 ,且︱
,且︱ ︱
︱ ,则
,则 的坐标为( )
的坐标为( )
A. | B. | C. | D. |
已知平面向量
 ,
,
 ,且
,且 ,则向量
,则向量 ( )
( )
A. | B. | C. | D. |
向量 ,向量,
,向量, 则
则 的最大值,最小值分别是( )
的最大值,最小值分别是( )
A. | B. | C. | D. |
已知平面向量 ,
, ,且
,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知点
A. | B. |
C.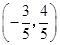 | D. |