题目内容
抛物线 上一点到直线
上一点到直线 的距离最短,则该点的坐标是( )
的距离最短,则该点的坐标是( )
A.(1, 2) B.(0,
0) C.( , 1) D.(1, 4)
, 1) D.(1, 4)
【答案】
C
【解析】本试题主要是考查了圆锥曲线上的点到直线的距离的最短的点问题的运用。
因为根据原函数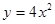 可知导数为y'=8x,由抛物线上点到直线
可知导数为y'=8x,由抛物线上点到直线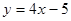 的距离最短,可知该点的导数值为4,即为在该点切线的斜率,即为8x=4得x=
的距离最短,可知该点的导数值为4,即为在该点切线的斜率,即为8x=4得x=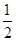
故抛物线的斜率为4的切线的切点坐标是(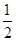 ,1),,该点到直线y=4x-5的距离是最短.,故选C.
,1),,该点到直线y=4x-5的距离是最短.,故选C.
关键是利用导数的几何意义得到该点的斜率即为导数值,进而得到点的坐标。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 上一点到直线
上一点到直线 的距离最短的点的坐标是 ( )
的距离最短的点的坐标是 ( ) ) C.
) C. D.(2,4)
D.(2,4) 上一点到直线
上一点到直线 的距离最短的点的坐标是 ( )
的距离最短的点的坐标是 ( ) ) C.
) C. D.(2,4)
D.(2,4) 上一点
上一点 到直线
到直线 的距离是
的距离是 ,则点
,则点 上一点到直线
上一点到直线 的距离最短,则该点的坐标是 (
)
的距离最短,则该点的坐标是 (
) B.
B. C.
C. D.
D.