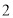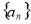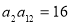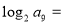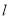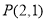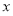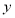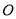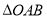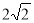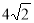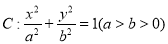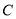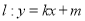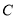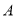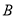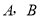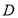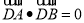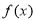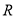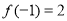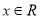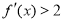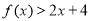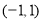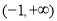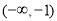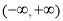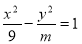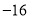题目内容
命题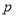 : 关于
: 关于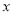 的不等式
的不等式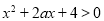 ,对一切
,对一切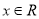 恒成立; 命题
恒成立; 命题 : 函数
: 函数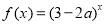 在
在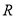 上是增函数.若
上是增函数.若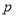 或
或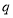 为真,
为真, 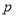 且
且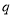 为假,求实数
为假,求实数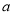 的取值范围.
的取值范围.
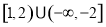 .
.
【解析】
试题分析:先根据不等式恒成立问题以及二次函数的图像与性质求出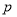 为真时的
为真时的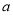 的取值范围,再根据指数函数的图像与性质求出
的取值范围,再根据指数函数的图像与性质求出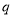 为真时的
为真时的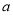 的取值范围.根据已知条件“
的取值范围.根据已知条件“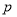 或
或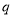 为真,
为真,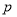 且
且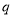 为假”可知,
为假”可知,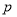 与
与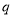 一真一假,那么分别求出“
一真一假,那么分别求出“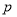 真
真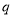 假”和“
假”和“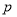 假
假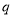 真”情况下的
真”情况下的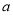 的取值范围,两种情况下的
的取值范围,两种情况下的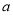 的取值范围取并集即可.
的取值范围取并集即可.
试题解析:由于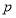 为真,故有
为真,故有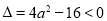 解得
解得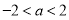 2分
2分
再由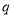 为真,可得
为真,可得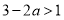 解得
解得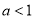 4分
4分
因为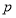 或
或 为真,
为真,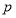 且
且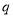 为假
为假

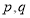 一真一假 6分
一真一假 6分
当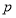 真
真 假时,
假时,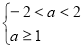
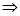
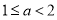
当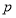 假
假 真时,
真时,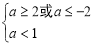
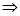
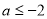 10分
10分

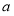 的取值范围为
的取值范围为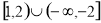 12分.
12分.
考点:1.二次不等式;2.指数函数的图像与性质;3.逻辑联结词.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目