题目内容
选做题
如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B=60°，F在AC上，且AE=AF．
（1）证明：B，D，H，E四点共圆；
（2）证明：CE平分∠DEF．
如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B=60°，F在AC上，且AE=AF．
（1）证明：B，D，H，E四点共圆；
（2）证明：CE平分∠DEF．
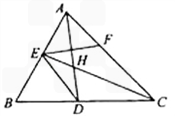
解：（I）在△ABC中，
因为∠B=60°所以∠BAC+∠HCA=120°
因为AD，CE是角平分线所以∠AHC=120°
于是∠EHD=∠AHC=120°
因为∠EBD+∠EHD=180°，所以B，D，H，E四点共圆
（II）连接BH，则BH为∠ABC得平分线，
得∠HBD=30°
由（I）知B，D，H，E四点共圆所以∠CED=HBD=30°
又∠AHE=∠EBD=60°
由已知可得，EF⊥AD，
可得∠CEF=30°
所以CE平分∠DEF
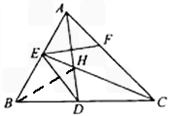
因为∠B=60°所以∠BAC+∠HCA=120°
因为AD，CE是角平分线所以∠AHC=120°
于是∠EHD=∠AHC=120°
因为∠EBD+∠EHD=180°，所以B，D，H，E四点共圆
（II）连接BH，则BH为∠ABC得平分线，
得∠HBD=30°
由（I）知B，D，H，E四点共圆所以∠CED=HBD=30°
又∠AHE=∠EBD=60°
由已知可得，EF⊥AD，
可得∠CEF=30°
所以CE平分∠DEF
练习册系列答案
相关题目
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.
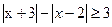的解集为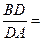
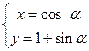（a为参数）以原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为
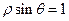，则直线l与圆C的交点的直角坐标系为____
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
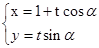（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.