题目内容
(本小题12分)
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,

(1)求函数 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。
(2)根据图像写出的单调区间和值域。
已知函数
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,

(1)求函数
 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。(2)根据图像写出的单调区间和值域。
(1) 
(2) 函数 的单调递增区间为
的单调递增区间为
单调递减区间为 ,函数
,函数 的值域为
的值域为 —
—

(2) 函数
 的单调递增区间为
的单调递增区间为
单调递减区间为
 ,函数
,函数 的值域为
的值域为 —
—试题分析:解:(1)由
 ,当
,当 ,
,
又函数
 为偶函数,
为偶函数, —————————————3’
—————————————3’故函数的解析式为
 —————————————4’
—————————————4’(2)由函数的图像可知,函数
 的单调递增区间为
的单调递增区间为
单调递减区间为
 ,函数
,函数 的值域为
的值域为 ——————12’
——————12’点评:解决该试题的关键是利用对称性作图,并能加以结合单调性的性质来求解最值。属于基础题。

练习册系列答案
相关题目
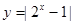 在区间
在区间 上不单调,则
上不单调,则 的取值范围 ;
的取值范围 ;
 的图像大致为 ( )
的图像大致为 ( )
 的图象大致是( )
的图象大致是( )

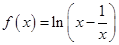 的图象是
的图象是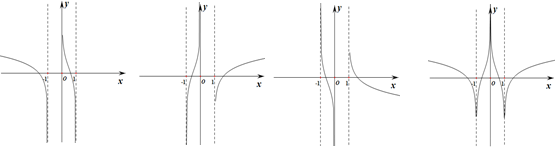
 的定义域为
的定义域为 ,若
,若 时,
时,

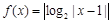 ,且关于x的方程
,且关于x的方程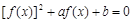 有6个不同的实数解,若最小实数解为
有6个不同的实数解,若最小实数解为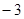 ,则
,则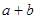 的值为( )
的值为( ) ,则函数
,则函数 与
与 的图象是 ( )
的图象是 ( )