Question

教科书上例1，探究有没有其他的解法？

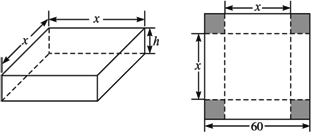
如图，在边长为60 cm的正方形铁片的四角上切去相等的正方形，再把它的边沿虚线折起，做成一个无盖的方底箱子，箱底的边长是多少时，箱子的容积最大？最大容积是多少？

Answer 1

答案：
解析：

探究：思路一：设箱底高为x cm，则箱底边长为(60－2x)cm，则得箱子容积V是x的函数： 　　V(x)＝(60－2x)2·x(0＜x＜30)＝(60－2x)(60－2x)·4x． 　　由60－2x＝4xx＝10． 　　思路二：用初等方法解答：设箱底边长为x cm，则箱高h＝cm，得箱子容积V是箱底边长x的函数： 　　V(x)＝(60－x)·x·x＝2(60－x)·， 　　由60－x＝x＝40．