题目内容
直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格点函数、下列函数:①f(x)=sinx;②f(x)=π(x-1)2+3;③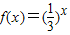 ;④f(x)=log0.6x其中是一阶格点函数的有( )
;④f(x)=log0.6x其中是一阶格点函数的有( )A.①②
B.①④
C.①②④
D.①②③④
【答案】分析:根据“格点”的定义,若①中X取非0整数,则f(x)必要无理数,故可以判断f(x)=π(x-1)2-1只有(0,-1)一个格点;②中根据指数函数性质,当X为小于等于1的整数时,f(x)均为整数,则f(x)=20101-x有无数个格点,③x=0时,f(x)=1,x=-1时,f(x)=3,故f(x)=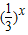 有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
;而④中,X为任意整数(x)都为整数.由此易得答案.
解答:解:①中,∵x=0,f(x)=0;当x≠0,x∈Z时,f(x)均为非整数,
∴f(x)=sinx只有(0,0)一个格点,为“一阶格点”函数;
②中,∵x=1时,f(x)=3.当x≠0,x∈Z时,f(x)均为非整数,
故f(x)=π(x-1)2+3只有(1,3)一个格点
为“一阶格点”函数;
③中,∵x=0时,f(x)=1,x=-1时,f(x)=3,
故f(x)=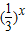 有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
④中,∵x=1时,f(x)=0
当x≠0,x∈Z+时,f(x)均为非整数,
故f(x)=ln(x+1)只有(0,0)一个格点
为“一阶格点”函数.
故选D.
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.
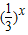 有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
有(0,1),(-1,3)等多个格点,为“一阶格点”函数;;而④中,X为任意整数(x)都为整数.由此易得答案.
解答:解:①中,∵x=0,f(x)=0;当x≠0,x∈Z时,f(x)均为非整数,
∴f(x)=sinx只有(0,0)一个格点,为“一阶格点”函数;
②中,∵x=1时,f(x)=3.当x≠0,x∈Z时,f(x)均为非整数,
故f(x)=π(x-1)2+3只有(1,3)一个格点
为“一阶格点”函数;
③中,∵x=0时,f(x)=1,x=-1时,f(x)=3,
故f(x)=
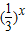 有(0,1),(-1,3)等多个格点,为“一阶格点”函数;
有(0,1),(-1,3)等多个格点,为“一阶格点”函数;④中,∵x=1时,f(x)=0
当x≠0,x∈Z+时,f(x)均为非整数,
故f(x)=ln(x+1)只有(0,0)一个格点
为“一阶格点”函数.
故选D.
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.

练习册系列答案
相关题目