题目内容
若 ,且
,且 ,则
,则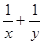 的最小值为
的最小值为
 ,且
,且 ,则
,则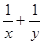 的最小值为
的最小值为 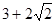
试题分析:因为
 ,且
,且 ,,那么
,,那么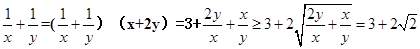 ,当
,当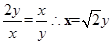 时等号成立,故可知最小值为
时等号成立,故可知最小值为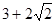
点评:解决的关键是根据和定则积有最大值来求解,属于基础题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
 ,且
,且 ,则
,则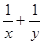 的最小值为
的最小值为 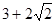
 ,且
,且 ,,那么
,,那么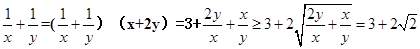 ,当
,当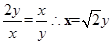 时等号成立,故可知最小值为
时等号成立,故可知最小值为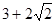

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案