题目内容
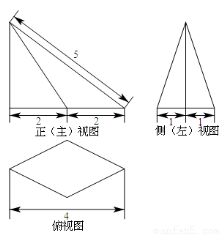
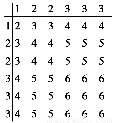
设x1＝18，x2＝19，x3＝20，x4＝21，x5＝22，将这5个数依次输入下面的程序框图运行，则输出S的值及其统计意义分别是( )
A．S＝2，这5个数据的方差 B．S＝2，这5个数据的平均数
C．S＝10，这5个数据的方差 D．S＝10，这5个数据的平均数
A
【解析】据已知数据可得其均值
＝
＝20，而框图输出S＝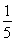
[(x1－20)2＋(x2－20)2＋…＋(x5－20)2]＝2，S的统计意义是此5个数据的方差，故选A
一次射击训练，某小组的成绩只有7环、8环、9环三种情况，且该小组的平均成绩为8.15环，设该小组成绩为7环的有x人，成绩为8环、9环的人数情况见下表：
环数(环) | 8 | 9 |
人数(人) | 7 | 8 |
那么x＝________.
甲、乙两所学校高三年级分别有1 200人，1 000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校：
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
(1)计算x，y的值；
(2)若规定考试成绩在[120,150]内为优秀，请分别估计两所学校数学成绩的优秀率；
(3)由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
参考数据与公式：由列联表中数据计算K2＝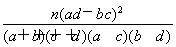
. ?
临界值表
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
