题目内容
例题:已知cosα=| 1 |
| 7 |
| 11 |
| 14 |
| π |
| 2 |
分析:先根据α和β的范围利用同角三角函数基本关系求得sinα和cos(α+β),进而利用两角和公式根据cosβ=cos(α-α+β)求得答案.
解答:解:∵α,β∈(0,
)
∴≤α+β≤π
∴sinα=
=
,sin(α+β)=
=
∴cosβ=cos(α-α+β)=cosαcos(α+β)+sinαsin(α+β)=
故答案为:
| π |
| 2 |
∴≤α+β≤π
∴sinα=
1-
|
4
| ||
| 7 |
1-(
|
5
| ||
| 14 |
∴cosβ=cos(α-α+β)=cosαcos(α+β)+sinαsin(α+β)=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查了同角三角函数基本关系的应用,两角和与差的余弦函数.要特别注意三角函数值的正负的判定.

练习册系列答案
相关题目
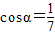 ,
,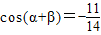 ,且
,且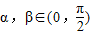 ,求cosβ的值为 .
,求cosβ的值为 .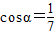 ,
,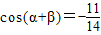 ,且
,且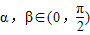 ,求cosβ的值为 .
,求cosβ的值为 .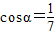 ,
,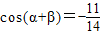 ,且
,且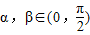 ,求cosβ的值为 .
,求cosβ的值为 .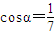 ,
, ,且
,且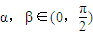 ,求cosβ的值为 .
,求cosβ的值为 .