题目内容
已知角α是第三象限角,且f(α)=| sin(π-α)cos(2π-α)tan(-α-π) |
| tan(π+α)sin(-π-α) |
(1)化简f(α);
(2)若cos(α-
| 3π |
| 2 |
| 1 |
| 5 |
(3)若cos(α+
| π |
| 4 |
| 3 |
| 5 |
分析:(1)利用诱导公式对函数解析式化简整理求得f(α)=-cosα.
(2)利用诱导公式求得sinα的值,进而利用同角三角函数的基本关系和α的范围,求得cosα的值,代入函数解析式中求得答案.
(3)根据α的范围确定α+
的范围,进而利用同角三角函数的基本关系求得sin(α+
)的值,进而根据cosα=cos[(α+
)-
]利用余弦的两角和公式求得cosα的值,代入函数解析式,求得答案.
(2)利用诱导公式求得sinα的值,进而利用同角三角函数的基本关系和α的范围,求得cosα的值,代入函数解析式中求得答案.
(3)根据α的范围确定α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:解:(1)f(α)=
=-
=-cosα
(2)∵cos(α-
)=
∴sinα=-
又∵α是第三象限角
∴cosα=-
∴f(α)=-cosα=
(3)∵α是第三象限角
∴2kπ+
π<α<2kπ+
π,k∈z
又∵cos(α+
)=
∴sin(α+
)=-
∴cosα=cos[(α+
)-
]=cos(α+
)cos
+sin(α+
)sin
=-
∴f(α)=-cosα=
| sin(π-α)cos(2π-α)tan(-α-π) |
| tan(π+α)sin(-π-α) |
| sinαcosαtanα |
| tanαsinα |
(2)∵cos(α-
| 3π |
| 2 |
| 1 |
| 5 |
∴sinα=-
| 1 |
| 5 |
又∵α是第三象限角
∴cosα=-
2
| ||
| 5 |
∴f(α)=-cosα=
2
| ||
| 5 |
(3)∵α是第三象限角
∴2kπ+
| 5 |
| 4 |
| 7 |
| 4 |
又∵cos(α+
| π |
| 4 |
| 3 |
| 5 |
∴sin(α+
| π |
| 4 |
| 4 |
| 5 |
∴cosα=cos[(α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 10 |
∴f(α)=-cosα=
| ||
| 10 |
点评:本题主要考查了同角三角函数的基本关系的应用,诱导公式的化简求值.解题的过程中注意角的范围,进而正确判断出三角函数正负值.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,且
,且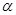 是第三象限角,求
是第三象限角,求 ,
,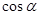 . (12分)
. (12分)