题目内容
某科技公司遇到一个技术难题,紧急成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期满就攻克技术难题的小组给予奖励.已知此技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.(1)设ξ为攻关期满时获奖的攻关小组数,求ξ的分布列及Eξ;
(2)设η为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数f(x)=|η-
 |x在定义域内单调递减”为事件C,求事件C的概率.
|x在定义域内单调递减”为事件C,求事件C的概率.
【答案】分析:(1)ξ为攻关期满时获奖的攻关小组数,则ξ的所有可能取值为0,1,2.根据变量结合的事件和相互独立事件同时发生的概率,写出变量的概率,写出分布列.
(2)根据获奖攻关小组数的可能取值为0,1,2,得到相对应没有获奖的攻关小组的取值为2,1,0,得到η的可能取值为0,4.写出函数式,根据函数的单调性得到结果.
解答:解:(1)记“甲攻关小组获奖”为事件A,则P(A)= ,记“乙攻关小组获奖”为事件B,则P(B)=
,记“乙攻关小组获奖”为事件B,则P(B)=
由题意,ξ的所有可能取值为0,1,2.
P(ξ=0)=(1- )(1-
)(1- )=
)=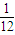
P(ξ=1)=(1- )×
)×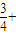
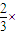 (1-
(1- )=
)=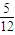
P(ξ=2)=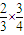 =
=
∴ξ的分布列为:
∴Eξ=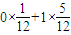 +
+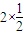 =
=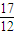
(2)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.
∴η的可能取值为0,4.
当η=0时,f(x)=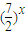 在定义域内是增函数.
在定义域内是增函数.
当η=4时,f(x)=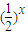 在定义域内是减函数.
在定义域内是减函数.
∴P(C)=P(η=4)= =
=
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查函数的单调性,考查指数函数的单调性,本题是一个综合题目.
(2)根据获奖攻关小组数的可能取值为0,1,2,得到相对应没有获奖的攻关小组的取值为2,1,0,得到η的可能取值为0,4.写出函数式,根据函数的单调性得到结果.
解答:解:(1)记“甲攻关小组获奖”为事件A,则P(A)=
 ,记“乙攻关小组获奖”为事件B,则P(B)=
,记“乙攻关小组获奖”为事件B,则P(B)=
由题意,ξ的所有可能取值为0,1,2.
P(ξ=0)=(1-
 )(1-
)(1- )=
)=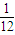
P(ξ=1)=(1-
 )×
)×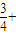
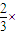 (1-
(1- )=
)=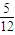
P(ξ=2)=
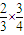 =
=
∴ξ的分布列为:
| ξ | 1 | 2 | |
| P | 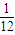 | 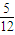 |  |
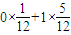 +
+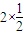 =
=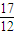
(2)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.
∴η的可能取值为0,4.
当η=0时,f(x)=
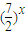 在定义域内是增函数.
在定义域内是增函数.当η=4时,f(x)=
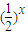 在定义域内是减函数.
在定义域内是减函数.∴P(C)=P(η=4)=
 =
=
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查函数的单调性,考查指数函数的单调性,本题是一个综合题目.

练习册系列答案
相关题目
 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
. |x在定义域内单调递减”为事件C,求事件C的概率.
|x在定义域内单调递减”为事件C,求事件C的概率. ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
. |x在定义域内单调递减”为事件C,求事件C的概率.
|x在定义域内单调递减”为事件C,求事件C的概率.