题目内容
椭圆M: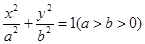 长轴上的两个顶点为
长轴上的两个顶点为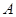 、
、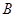 ,点P为椭圆M上除
,点P为椭圆M上除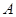 、
、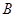 外的一个动点,若
外的一个动点,若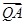 ·
·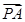 =0,
=0,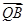 ·
·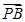 =0,则动点Q在下列哪种曲线上( )
=0,则动点Q在下列哪种曲线上( )
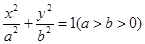 长轴上的两个顶点为
长轴上的两个顶点为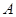 、
、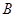 ,点P为椭圆M上除
,点P为椭圆M上除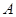 、
、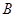 外的一个动点,若
外的一个动点,若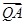 ·
·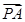 =0,
=0,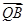 ·
·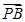 =0,则动点Q在下列哪种曲线上( )
=0,则动点Q在下列哪种曲线上( )| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
B
试题分析:A坐标为(-a,0),B坐标为(a,0)
设Q坐标为(m,n),P坐标为(s,t)
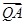 ·
·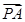 =(-a-m)(-a-s)+(-n)(-t)=0
=(-a-m)(-a-s)+(-n)(-t)=0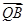 ·
·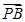 =(a-m)(a-s)+(-n)(-t)=0
=(a-m)(a-s)+(-n)(-t)=0解得:s=-m,t=
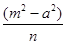
又P在M上,∴s=asint,t=bcost
解得:m=-asint,n=-
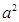 cost/b
cost/b即:
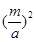 +
+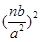 =1
=1所以点Q(m,n)应该是在一个椭圆上
点评:本试题利用数量积为姆拜哦,结合坐标法来表示向量,然后得到坐标的关系式,进而确定出点Q的坐标满足的关系式,属于中档题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
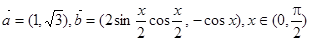 ,若
,若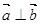 ,则
,则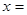
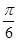
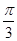
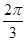
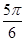
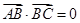 ,
,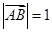 ,
,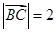 ,
,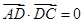 ,则
,则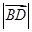 的最大值为( )
的最大值为( )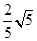
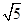
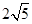
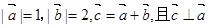 ,则向量
,则向量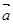 与
与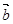 的夹角为( )
的夹角为( )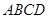 的边长为
的边长为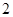 ,
,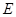 是
是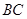 的中点,则
的中点,则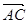 ·
·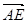 = .
= .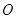 为坐标原点,
为坐标原点,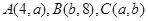 ,
,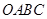 是平行四边形,求
是平行四边形,求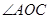 的大小;
的大小;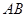 中点为
中点为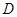 ,
,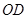 与
与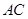 交于
交于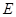 ,求
,求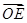 .
. ,
,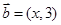 ,且
,且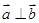 ,则实数
,则实数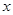 的值为
的值为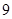
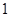
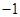
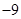
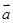 =(-3,2,5),b=(1,x,-1),且
=(-3,2,5),b=(1,x,-1),且 ,则x的值为
,则x的值为