题目内容
对一切实数x，不等式x2＋a|x|＋1≥0恒成立，则实数a的取值范围是
( )
( )
| A．[－2，＋∞) | B．(－∞－2) |
| C．[－2,2] | D．[0，＋∞) |
A
由题意可求出a的表达式，利用均值不等式求出a的取值范围．
解：据已知可得a≥-|x|-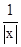
=-(|x|+|
|)，
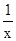据均值不等式|x|+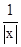≥2?-(| x|+|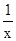|)≤-2，
故若使原不等式恒成立，只需a≥-2即可．
故选A．
解：据已知可得a≥-|x|-
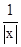=-(|x|+|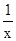|)，据均值不等式|x|+
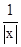≥2?-(| x|+|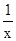|)≤-2，故若使原不等式恒成立，只需a≥-2即可．
故选A．
练习册系列答案
相关题目
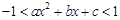的解集为
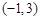，则实数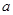
的取值范围是 
的不等式
在区间
上有解，求
的取值范围.
的解集为（ ）
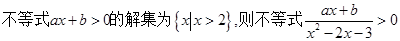
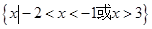
的解集为A，不等式
的解集为B，
B；
的解集是A
的解集.
对于
恒成立，那么
的取值范围
>0的解集为