题目内容
设圆台的高为3,其轴截面(过圆台轴的截面)如图所示,母线A1A与底面圆的直径AB的夹角为60°,在轴截面中A1B⊥A1A,求圆台的体积V.

分析:根据圆台的轴截面,求出圆台的上底半径和下底半径,然后利用圆台的体积公式求体积.
解答:解:设AB的中点为O,作A1D⊥AB,则A1D=3,
∵A1B⊥A1A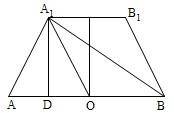
∴在直角△A1AB中,A1O=
AB=AO,
又∵∠A1AB=60°
∴△A1AO为等边三角形.
∴在△A1AO中A1D=
AO=3,得AO=2
,
设圆台的上、下底面半径分别为r,R.
∴R=AO=2
,r=DO=
A0=
,
∴上、下底面面积分别为:S'=πr2=3π,S=πR2=12π,
∴体积v=
(S′+S+
)•A1D=
(3π+
+12π)×3=21π.
∴圆台的体积为21π.
∵A1B⊥A1A

∴在直角△A1AB中,A1O=
| 1 |
| 2 |
又∵∠A1AB=60°
∴△A1AO为等边三角形.
∴在△A1AO中A1D=
| ||
| 2 |
| 3 |
设圆台的上、下底面半径分别为r,R.
∴R=AO=2
| 3 |
| 1 |
| 2 |
| 3 |
∴上、下底面面积分别为:S'=πr2=3π,S=πR2=12π,
∴体积v=
| 1 |
| 3 |
| S′S |
| 1 |
| 3 |
| 36π2 |
∴圆台的体积为21π.
点评:本题主要考查三视图的应用,以及圆台的体积公式,要求熟练掌握规则几何体的体积公式.

练习册系列答案
相关题目
