题目内容
(20分)在一次实战军事演习中,红方的一条直线防线上设有20个岗位。为了试验5种不同新式武器,打算安排5个岗位配备这些新式武器,要求第一个和最后一个岗位不配备新式武器,且每相邻5个岗位至少有一个岗位配备新式武器,相邻两个岗位不同时配备新式武器,问共有多少种配备新式武器的方案?解析: 设20个岗位按先后排序为1,2,,… ,20,且设第k种新式武器设置的序号为![]()
![]() 。令
。令![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,则有
,则有
![]() (*)
(*)
其中![]()
![]() ,
,![]() 。 -------------------------------------- 5分
。 -------------------------------------- 5分
作代换 ![]()
![]() ,
,![]() ,从而有
,从而有
![]() (**)
(**)
其中 ![]()
![]() 。 ---------------------------------------------------------- 10分
。 ---------------------------------------------------------- 10分
现求解问题(**):
方法一: 设I为![]() 的正整数解的全体,
的正整数解的全体,![]() 为I中
为I中![]() 满足
满足![]() 的解的全体。则
的解的全体。则
![]()
上式成立的原因是![]() ,因为没有同时满足
,因为没有同时满足![]() ,
,![]() ,
,![]() 的
的![]() 的正整数组。所以
的正整数组。所以
![]() . -------------- 15分
. -------------- 15分
方法二 :问题(**)的解数等于![]() 展开式中
展开式中![]() 的系数。
的系数。
而![]() ,
,
故只须求![]() 展开式中
展开式中![]() 的系数。
的系数。
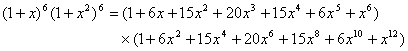
因此![]() 的系数为 6×15+20×20+6×15 = 580。 ----------------------------------------- 15分
的系数为 6×15+20×20+6×15 = 580。 ----------------------------------------- 15分
因为5种新式武器各不相同,互换位置得到不同的排列数,所以配备新式武器的方案数等于
![]() 。 ------------------------------------------ 20分
。 ------------------------------------------ 20分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目