题目内容
证明下列三角恒等式：
（1）
=tan2θ；
（2）
=
．
（1）
| 1-cos2θ |
| 1+cos2θ |
（2）
| 1-2sinθcosθ |
| cos2θ-sin2θ |
| 1-tanθ |
| 1+tanθ |
证明：（1）等式的左边=
=
=
=tan2θ=右边，故等式成立．
（2）等式的左边=
=
=
=
=右边，故等式成立．
| 1-cos2θ |
| 1+cos2θ |
| 1-(1-2sin2θ) |
| 1+(2cos2θ-1) |
| 2sin2θ |
| 2cos2θ |
（2）等式的左边=
| 1-2sinθcosθ |
| cos2θ-sin2θ |
| (cosθ-sinθ)2 |
| (cosθ+sinθ)(cosθ-sinθ) |
| cosθ-sinθ |
| cosθ+sinθ |
| 1-tanθ |
| 1+tanθ |
=右边，故等式成立．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
；
．
.
.
；
．
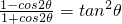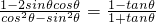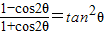