题目内容
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
(1)0.24
(2)
(2)
| ξ | 0 | 2 |
| P | 0.24 | 0.76 |
(1)设该学生选修课程甲、乙、丙的概率分别为a,b,c,依题意得
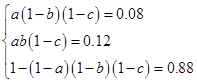
解得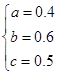
若函数f(x)=x2+ξx为R上的偶函數,
则ξ=0.
当ξ=0时,表示该学生选修三门课程或三门课程都没选.
∴P(A)=P(ξ=0)=abc+(1-a)(1-b)(1-c)
=0.4×0.5×0.6+(1-0.4)(1-0.5)(1-0.6)=0.24.
∴事件A的概率为0.24.
(2)依题意知ξ=0,2.
则ξ的分布列为
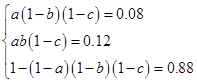
解得
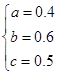
若函数f(x)=x2+ξx为R上的偶函數,
则ξ=0.
当ξ=0时,表示该学生选修三门课程或三门课程都没选.
∴P(A)=P(ξ=0)=abc+(1-a)(1-b)(1-c)
=0.4×0.5×0.6+(1-0.4)(1-0.5)(1-0.6)=0.24.
∴事件A的概率为0.24.
(2)依题意知ξ=0,2.
则ξ的分布列为
| ξ | 0 | 2 |
| P | 0.24 | 0.76 |

练习册系列答案
相关题目
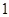 个、黄色球
个、黄色球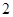 个、蓝色球
个、蓝色球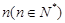 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得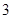 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出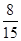 .
.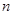 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出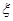 表示所摸
表示所摸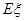 .
.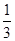 ,
,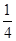 ,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.
,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.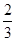 ,则甲以3∶1的比分获胜的概率为( )
,则甲以3∶1的比分获胜的概率为( )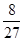
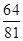
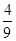
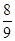
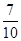 为概率的事件是( )
为概率的事件是( )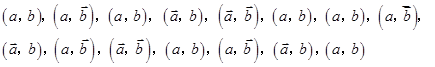
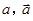 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;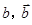 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
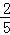
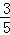
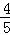
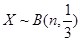 ,且
,且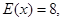 则
则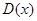 = ;
= ;